How to multiply polynomials
Distributive property for binomial multiplication
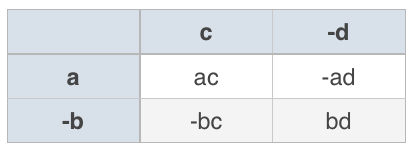
The distributive property can be used when multiplying polynomials. If you’re multiplying polynomials with more than two terms, a chart will be useful to organize your work.
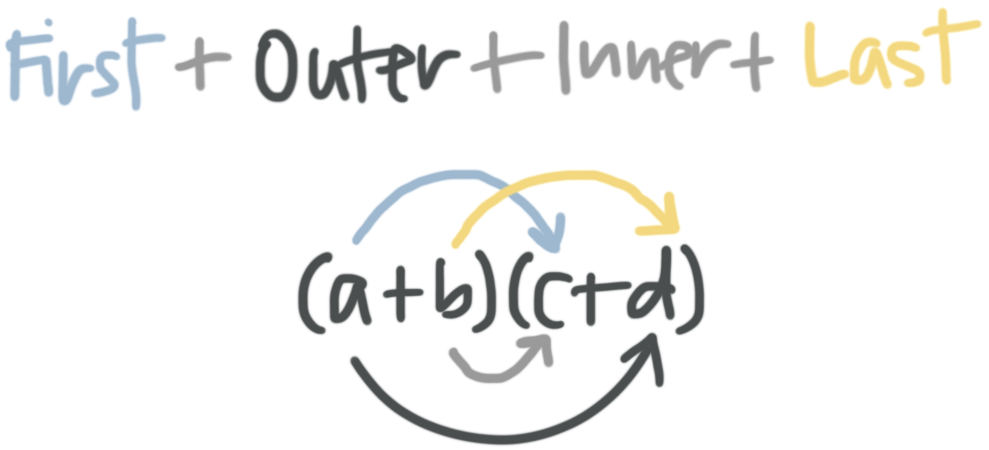
When each polynomial in a multiplication has two terms, it’s called binomial multiplication and we can use a special process called FOIL.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Binomial multiplication (using FOIL)
???(a+b)(c+d)=ac+ad+bc+bd???
???(a-b)(c-d)=ac-ad-bc+bd???
Notice that ???a??? is multiplied by both terms in the second set of parentheses and then ???b??? is multiplied by both terms in the second set of parentheses.
FOIL is a way to help you remember to multiply each term in the first set of parentheses by each term in the second set of parentheses. FOIL stands for Firsts, Outsides, Insides, Lasts, which is the order of the four terms in the result of the multiplication; it also indicates which terms in the given binomials are multiplied to produce each term in the result.
The Firsts are the first term in the first set of parentheses (which is ???a???) and the first term in the second set of parentheses (which is ), so the first term in the result (Firsts) is the product of ???a??? and ???c???, or ???ac???.
The Outsides are the outside term in the first set of parentheses (which is ???a???) and the outside term in the second set of parentheses (which is ???d???), so the second term in the result (Outsides) is the product of ???a??? and ???d???, or ???ad???.
Similarly, the Insides are ???b??? and ???c???, and the Lasts are ???b??? and ???d???, so the third term is the result (Insides) is ???bc???, and the fourth term in the result (Lasts) is ???bd???.
Binomial multiplication (using a chart)
A chart is another way to keep track of the different multiplications that are carried out during binomial and polynomial multiplication. It’s especially useful when multiplying polynomials with more than two terms.
???ac+ad+bc+bd???
???ac-ad-bc+bd???
How to multiply polynomials using the distributive property
Take the course
Want to learn more about Algebra 1? I have a step-by-step course for that. :)
Multiplying binomials using FOIL
Example
Expand the expression.
???(x+2)(x-7)???
Multiply the Firsts (???x??? and ???x???).
???x^2???
Multiply the Outsides (???x??? and ???-7???).
???-7x???
Multiply the Insides (???2??? and ???x???).
???2x???
Multiply the Lasts (???2??? and ???-7???).
???-14???
Write the four terms in the sum, and then combine like terms.
???x^2-7x+2x-14???
???x^2-5x-14???
Let’s try another example of multiplying polynomials.
A chart is another way to keep track of the different multiplications that are carried out during binomial and polynomial multiplication.
Example
Expand the expression.
???(x+3)^2???
This is “???(x+3)??? squared,” which means that the binomial ???(x+3)??? is to be multiplied by itself.
???(x+3)(x+3)???
Use FOIL to expand.
???x^2+3x+3x+9???
Combine like terms.
???x^2+6x+9???