How to graph parabolas
Complete the square to convert between standard and vertex form
In this lesson we’ll learn how to identify the characteristics of a parabola and go back and forth between algebraic form and graphical form.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
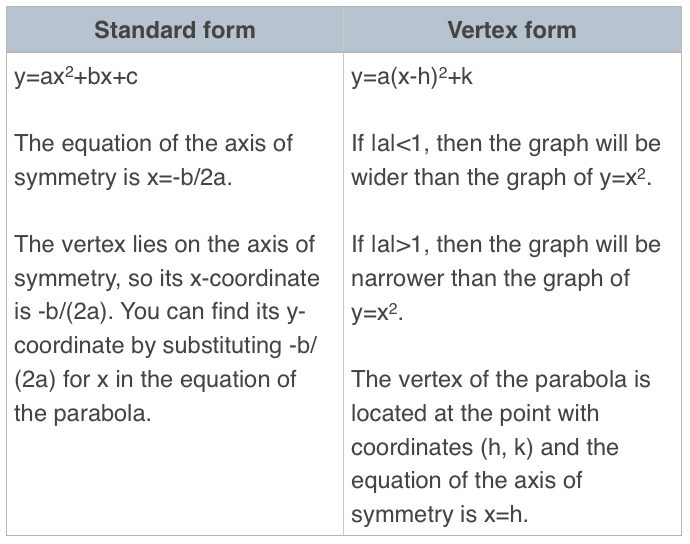
Quadratic equations create parabolas when they’re graphed, so they’re non-linear functions. There are two forms that are especially helpful when you want to know something about a parabola.
How to convert between Standard form and Vertex form:
To convert from Standard form into Vertex form, complete the square
To convert from Vertex form into Standard form, expand the square, then distribute and simplify
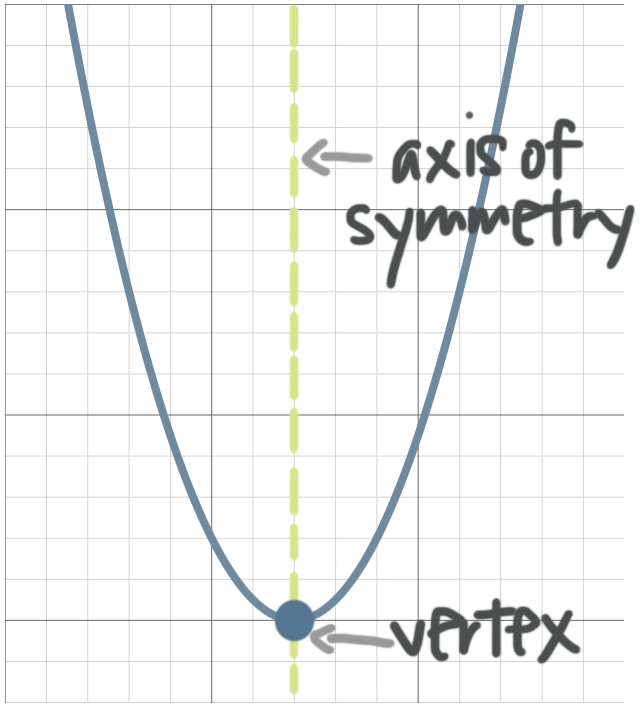
Let’s talk about the different parts of a parabola.
In both standard and vertex form, if ???a>0???, the parabola opens upwards and the vertex is a minimum value.
In both standard and vertex form, if ???a<0??? the parabola opens downwards and the vertex is a maximum value.
How to graph parabolas
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. :)
Converting from standard form to vertex form
Example
Write the equation in vertex form.
???y=2x^2+36x+170???
To convert to vertex form from standard from, you’ll need to complete the square.
Before we can do complete the square, we need to make the coefficient on the ???x^2??? term a positive ???1??? instead of ???2???, which we’ll do by factoring out a ???2??? from the first two terms.
???y=2x^2+36x+170???
???y=2(x^2+18x)+170???
Now taking the coefficient ???18??? on the first-degree ???x??? term and dividing it by ???2???, we get
???\frac{18}{2}=9???
Squaring the result gives
???(9)^2=81???
This is the value we have to add in order to complete the square. But we have to be careful. If we add ???81??? inside the parentheses on the right, the ???2??? outside of the parentheses applies to it, which means we’re actually adding a ???2(81)=162???. So we’ll have to subtract ???162??? from the outside of the parenthesis to keep the equation balanced.
???y=2(x^2+18x+81)-162+170???
???y=2(x^2+18x+81)+8???
Factor what’s inside the parentheses.
???y=2(x+9)(x+9)+8???
The vertex form of the equation is
???y=2(x+9)^2+8???
Quadratic equations create parabolas when they’re graphed, so they’re non-linear functions.
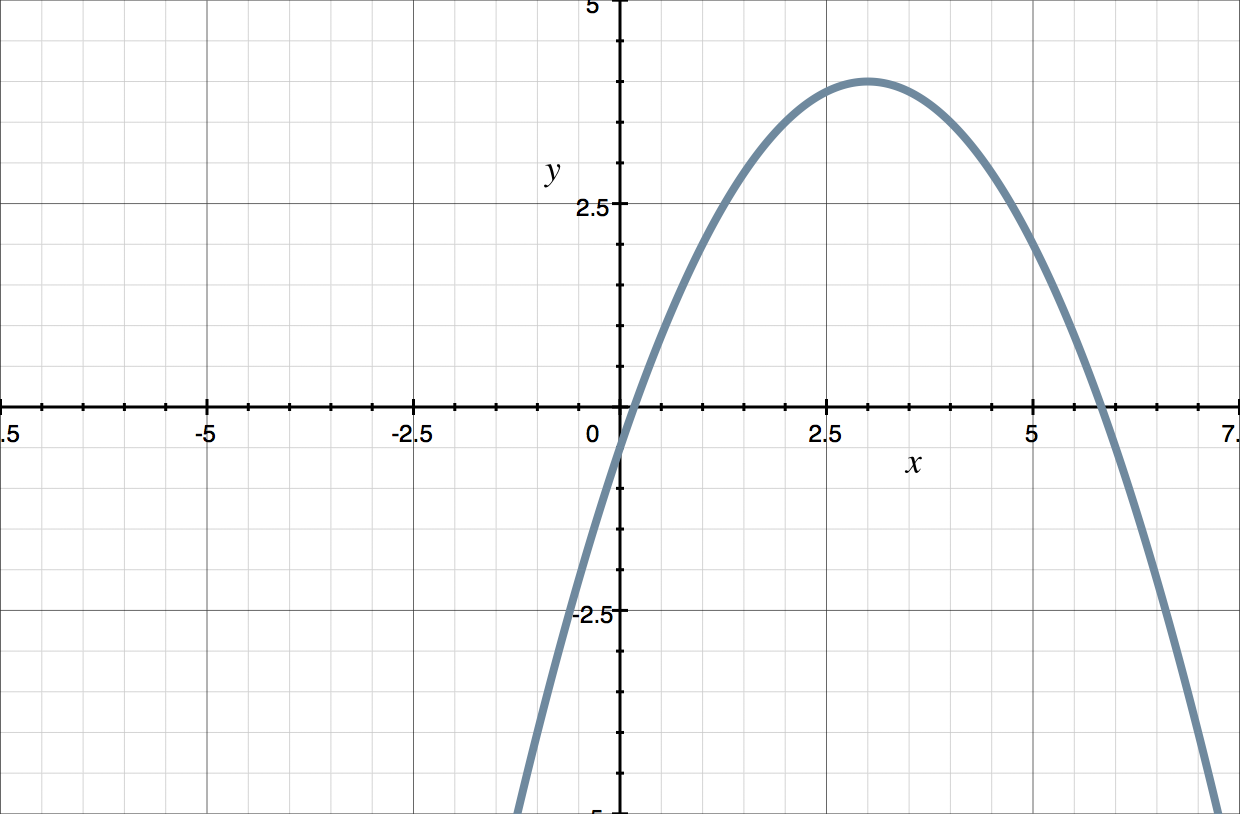
Example
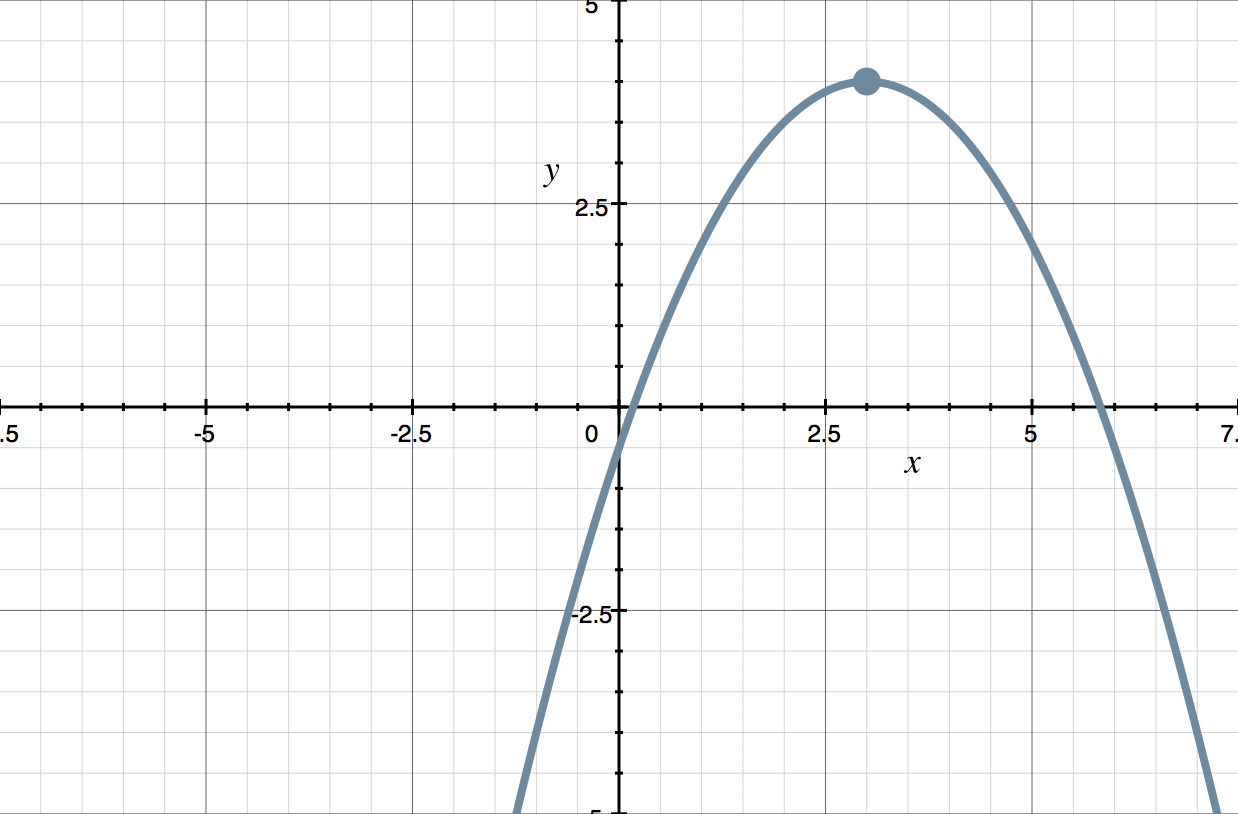
Assuming that the ???a??? term for the parabola shown in the graph is ???-1/2???, what is the equation of the parabola in standard form?
Remember the vertex form of a parabola is ???y=a(x-h)^2+k???, where ???(h,k)??? is the vertex.
We know that ???a=-1/2??? and we can read the vertex from the graph. The vertex is ???(3,4)???.
So we know ???h=3??? and ???k=4???. Let’s put what we know into the vertex form for the equation of a parabola.
???y=a(x-h)^2+k???
???y=-\frac{1}{2}(x-3)^2+4???
Now we want to go from vertex form to standard form, so we’ll expand the square:
???y=-\frac{1}{2}(x-3)(x-3)+4???
???y=-\frac{1}{2}(x^2-6x+9)+4???
Distribute the ???-1/2???.
???y=-\frac{1}{2}x^2+3x-\frac{9}{2}+4???
???y=-\frac{1}{2}x^2+3x-\frac{1}{2}???