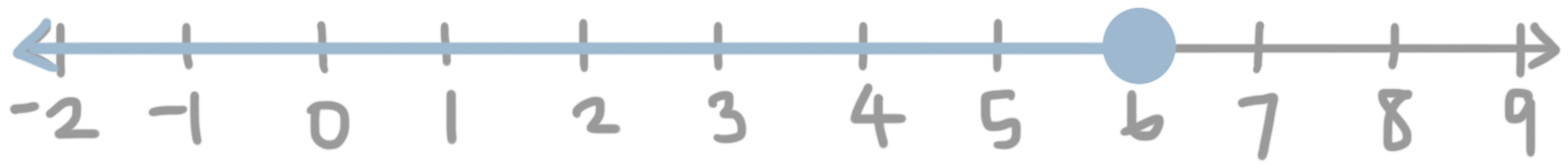Graphing conjunctions on a number line
How to identify conjunctions
Conjunctions are “and” statements. And you might be thinking, “What does that have to do with a number line?”
Well, there are times when we have two inequalities and we want to graph the points that satisfy both of them.
That’s where the “and” comes in: We want to graph the points that simultaneously satisfy both the first inequality and the second inequality.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
To graph a conjunction of two inequalities, we can first graph the inequalities separately and see where they overlap. Then we graph their conjunction on a separate number line, by including all the points that are on the graphs of both (not just one) of the inequalities (and no other points).
The four “simple” forms for a conjunction of two inequalities are as follows (where ???a??? and ???b??? are numbers):
???a\leq x\leq b???
???a\leq x<b???
???a<x\leq b???
???a<x<b???
Each of these may look like just a single inequality, but each of them is actually two inequalities. For example, ???1\leq x\leq 8??? is actually the two inequalities ???1\leq x??? and ???x\leq 8???.
Graphing conjunctions on a number line
Take the course
Want to learn more about Algebra 1? I have a step-by-step course for that. :)
Finding the overlap of two inequalities to create the conjunction
Example
Graph the conjunction.
???-3\leq x\leq6???
We need to graph the conjunction of the inequalities ???-3\leq x??? and ???x\leq 6???, but first let’s see how they graph separately.
The inequality ???-3\leq x??? can be turned around and written as ???x\geq -3???. So its graph has a solid circle at ???-3??? (because we have a greater than or equal to sign), and because of the greater than part of the inequality, the arrow goes to the right.
The graph of the inequality ???x\leq6??? has a solid circle at ???6??? (because we have a less than or equal to sign), and because of the less than part of the inequality, the arrow goes to the left.
To graph the conjunction of the two inequalities, we’ll graph only the overlap: a solid circle at ???-3??? (because ???-3??? is on the graphs of both of the inequalities), a solid circle at ???6??? (because ???6??? is on the graphs of both of the inequalities), and everything between ???-3??? and ???6???.
At times you may be given two separate inequalities and will need to graph their conjunction. To do that, you may need to solve one or both of the inequalities before you can write their conjunction in one of the four “simple” forms.
Then we graph their conjunction on a separate number line, by including all the points that are on the graphs of both (not just one) of the inequalities (and no other points).
Example
Graph the conjunction of the inequalities ???3x+1>5??? and ???2x-4\leq6???.
First, we’ll solve and graph the two inequalities separately. To begin solving ???3x+1>-5???, subtract ???1??? from both sides.
???3x+1>-5???
???3x+1-1>-5-1???
???3x>-6???
Now divide both sides by ???3???.
???\frac{3x}{3}>\frac{-6}{3}???
???x>-2???
The graph of the inequality ???x>-2??? has an open circle at ???-2??? (because we have just a greater than sign), and because it’s a greater than inequality, the arrow goes to the right.
To begin solving the inequality ???2x-4\leq 6???, add ???4??? to both sides.
???2x-4\leq 6???
???2x-4+4\leq 6+4???
???2x\leq 10???
Now divide both sides by ???2???.
???\frac{2x}{2}\leq \frac{10}{2}???
???x\leq 5???
The graph of the inequality ???x\leq 5??? has a solid circle at ???5??? (because we have a less than or equal to sign), and because of the less than part of the inequality, the arrow goes to the left.
We can combine the solutions we found (???x>-2??? and ???x\leq 5???) and write their conjunction in one of the four “simple” forms. If we take the first inequality (???x>-2???) and turn it around, we get ???-2<x???.
So the conjunction of the inequalities ???x>-2??? and ???x\leq 5??? can be written as
???-2<x\leq 5???
The graph of the conjunction will be the overlap of the graphs of the two separate inequalities: an open circle at ???-2??? (because ???-2??? isn’t on the graph of ???-2<x???), a solid circle at ???5??? (because ???5??? is on the graphs of both of the separate inequalities), and everything between ???-2??? and ???5???.
One thing you should be aware of is that there are pairs of inequalities whose solutions have nothing in common.
For example, suppose you were given two inequalities, ???x>8??? and ???x<-1???. In that case, the solution of their conjunction consists of all the numbers that are (simultaneously) greater than ???8??? and less than ???-1???. Well, no such number exists (no number that’s greater than ???8??? is also less than ???-1???), so the graph of the conjunction of the inequalities ???x>8??? and ???x<-1??? is just a bare number line, with nothing drawn on it.