Finding the area of a circle
Defining the area of a circle
In this lesson we’ll look at how to use the area formula for a circle.
Radius of a circle
The radius of a circle is the length from the center of a circle to a point on its circumference. This is a circle with radius, ???r???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
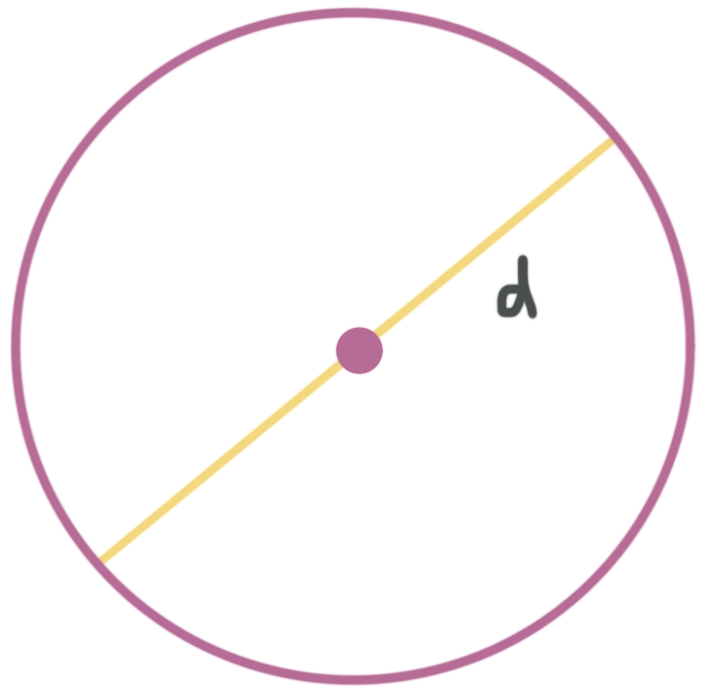
Diameter of a circle
The diameter of a circle is a special chord that passes through the center of the circle. It’s made of two radii.
???d=2r???
???r=\frac{1}{2}d???
This is a circle with diameter, ???d???.
Pi
Pi is a special number that describes the relationship between a circle’s circumference and the length of its diameter. It’s approximately equal to ???3.14???, which we write as ???\pi \approx 3.14???.
Area of a circle
The area of a circle is equal to ???\pi???, multiplied by the square of the radius.
???A=\pi r^2???
As with all areas, the units of the area are ???\text{units}^2???. Let’s start by working through an example.
How to find the area of a circle
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Calculating area from the diameter
Example
What is the area of the circle? Round your answer to the nearest hundredth.
The formula for the area is
???A=\pi {{r}^{2}}???
We’re given the diameter, and we need to find the radius. The radius is half of the diameter.
???r=\frac{1}{2}(5\text{ in})???
???r=2.5\text{ in}???
Now we can use the area formula.
???A=\pi (2.5\text{ in})^2???
???A=6.25\pi \text{ in}^2???
This is the exact answer. We’re asked to find the approximate answer so we’ll use the fact that ???\pi??? is about ???3.14???.
???A\approx 6.25(3.14)\text{ i}{{\text{n}}^{2}}???
???A\approx 19.63\text{ i}{{\text{n}}^{2}}???
Sometimes you’ll be given the area and asked to solve for something else.
Example
What is the radius of a circle with an area of ???75\pi \text{ c}{{\text{m}}^{2}}????
The formula for the area of a circle is ???A=\pi {{r}^{2}}???, and the area is ???75\pi \text{ c}{{\text{m}}^{2}}???.
???\pi {{r}^{2}}=75\pi \text{ c}{{\text{m}}^{2}}???
???{{r}^{2}}=75\text{ c}{{\text{m}}^{2}}???
???\sqrt{{{r}^{2}}}=\sqrt{75\text{ c}{{\text{m}}^{2}}}???
???r=\sqrt{75}\text{ cm}???
???r=\sqrt{25}\cdot \sqrt{3}\text{ cm}???
???r=5\sqrt{3}\text{ cm}???
Sometimes you’ll need to find the area of a composite figure that’s made of circles.
The diameter of a circle is a special chord that passes through the center of the circle. It’s made of two radii.
Example
What is the area of the large circle, but outside of the small circle? Leave your answer in terms of ???\pi???.
We need to find the area of the large circle and subtract the area of the small circle. The formula for the area of a circle is ???A=\pi {{r}^{2}}???, so we need to know the radius of each circle.
The radius of the larger circle is ???6??? feet, so the area of the larger circle is
???A=\pi \cdot {{6}^{2}}=36\pi \text{ f}{{\text{t}}^{2}}???
The small circle has a diameter of ???6??? feet, so its radius is ???r=6/2=3??? feet. So the area of the smaller circle is
???A=\pi \cdot {{3}^{2}}=9\pi \text{ f}{{\text{t}}^{2}}???
So the area of the larger circle, but outside of the smaller circle is
???36\pi \text{ f}{{\text{t}}^{2}}-9\pi \text{ f}{{\text{t}}^{2}}=27\pi \text{ f}{{\text{t}}^{2}}???