Factoring quadratic polynomials
Factoring a quadratic is like un-doing the “FOIL” process
Factoring of quadratic polynomials (second-degree polynomials) is done by “un-FOILing,” which means we start with the result of a FOIL problem and work backwards to find the two binomial factors.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
To factor a quadratic polynomial in which the ???x^2??? term has a coefficient of ???1??? and the constant term is nonzero (in other words, a quadratic polynomial of the form ???x^2+ax+b??? where ???b\ne0???), you’ll be considering pairs of factors of the last term (the constant term) and finding the pair of factors whose sum is the coefficient of the middle term (the ???x???-term).
How to factor quadratics
Take the course
Want to learn more about Algebra 1? I have a step-by-step course for that. :)
Looking for the factors of a constant
Example
Factor the quadratic polynomial.
???x^2-x-20???
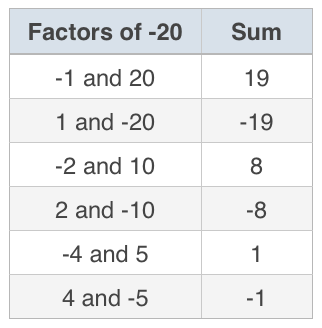
Start by listing the pairs of factors of the constant term, ???-20???, and their sums. We’re looking for the pair of factors whose sum is ???-1??? (the coefficient of the ???x???-term).
Since ???4??? and ???-5??? have a sum of ???-1???, they’re the factors we need. The answer is
???(x+4)(x-5)???
To check our answer, we can FOIL ???(x+4)(x-5)???.
???x^2-5x+4x-20???
???x^2-x-20???
Let’s try another example of factoring a quadratic polynomial.
Factoring of quadratic polynomials (second-degree polynomials) is done by “un-FOILing,” which means we start with the result of a FOIL problem and work backwards to find the two binomial factors.
Example
Factor the quadratic polynomial.
???x^2-8x+15???
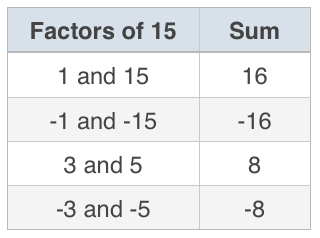
Start by listing the pairs of factors of ???15??? and their sums. We’re looking for the pair of factors whose sum is ???-8??? (the coefficient of the ???x???-term).
The factors ???-3??? and ???-5??? have a sum of ???-8???, so they’re the correct factors.
???(x-3)(x-5)???
To check our answer, we can FOIL ???(x-3)(x-5)???.
???x^2-5x-3x+15???
???x^2-8x+15???
If the coefficient of the ???x^2??? term in a quadratic polynomial is either ???-1??? or the greatest common factor of the polynomial, we can first factor that out and then use the procedure described above to factor what’s left over.
Example
Factor the quadratic polynomial.
???4x^2-20x+24???
The greatest common factor of this polynomial is ???4???, so we first factor out a ???4???.
???4(x^2-5x+6)???
Since ???(-3)(-2)=6??? and ???(-3)+(-2)=-5???, we see that ???x^2-5x+6??? can be factored as follows:
???(x-3)(x-2)???
So the given quadratic polynomial can be factored as
???4(x-3)(x-2)???
In later lessons, you’ll learn how to factor more complicated quadratic polynomials - those in which all of the following conditions are satisfied:
The coefficient of the ???x^2??? term is neither ???1??? nor ???-1???.
The coefficient of the ???x^2??? term isn’t the greatest common factor of the polynomial.
The constant term is nonzero.