Applying the isosceles triangle theorem
Defining isosceles triangles
In this lesson we’ll look at the definition of isosceles triangles and how to use the isosceles triangle theorem to solve problems.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Isosceles triangles
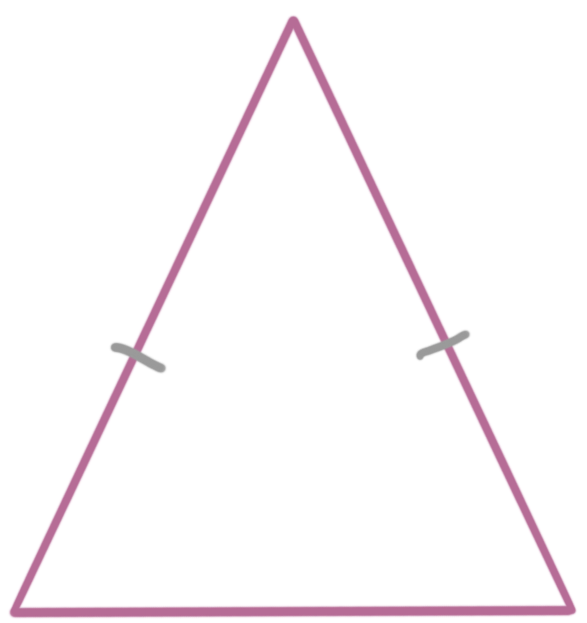
An isosceles triangle is a triangle with at least two equal sides.
If a triangle is equilateral, then it has three equal sides, which is therefore considered a special case of an isosceles triangle. The specific case of the equilateral triangle is the reason that the definition for an isosceles triangle includes the words “at least two equal sides.”
Isosceles triangle theorem
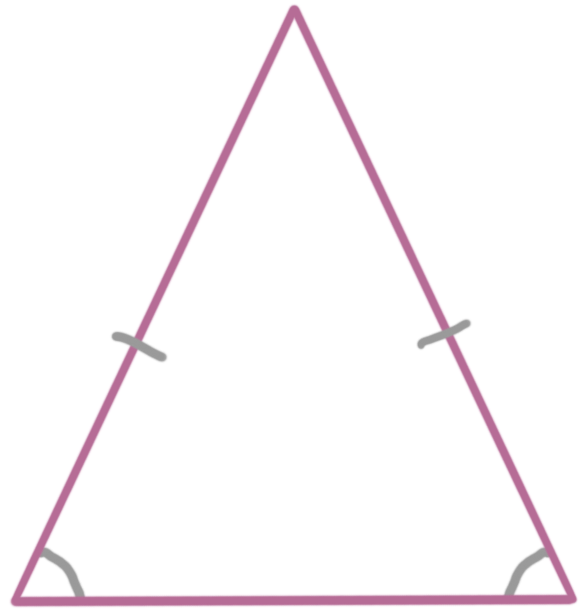
The isosceles triangle theorem says that if two sides of a triangle are congruent, then its base angles are congruent. The base angles are the angles that touch the non-congruent leg. So if you know this:
then you’ll also know this:
Converse of the isosceles triangle theorem
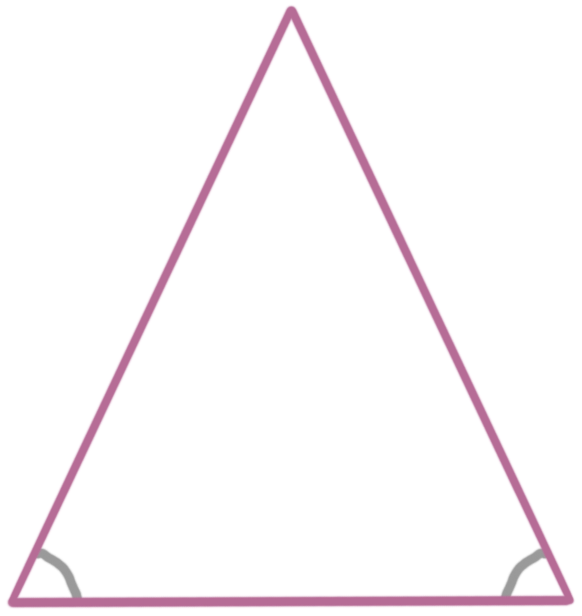
The converse of the isosceles triangle theorem just turns around the original theorem. It says that, if you know that two angles in a triangle are congruent, then those angles are the base angles and the triangle has a pair of congruent sides, which means it’s an isosceles triangle.
In other words, if you know this:
then you also know this:
Applying the isosceles triangle theorem
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Two more isosceles triangle examples
Example
What is the value of ???x????
The triangle is an isosceles triangle, so we know the base angles are congruent.
The angles of a triangle sum to ???180^\circ???, so we can set up an equation for the sum of the interior angles.
???x+x+100^\circ =180^\circ???
???2x+100^\circ =180^\circ???
???2x=80^\circ???
???x=40^\circ???
The specific case of the equilateral triangle is the reason that the definition for an isosceles triangle includes the words “at least two equal sides.”
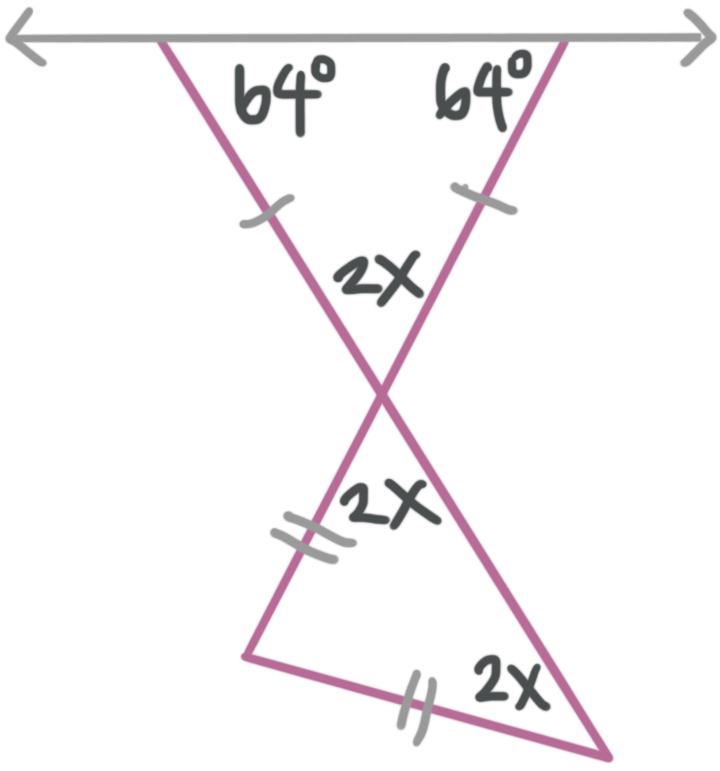
Example
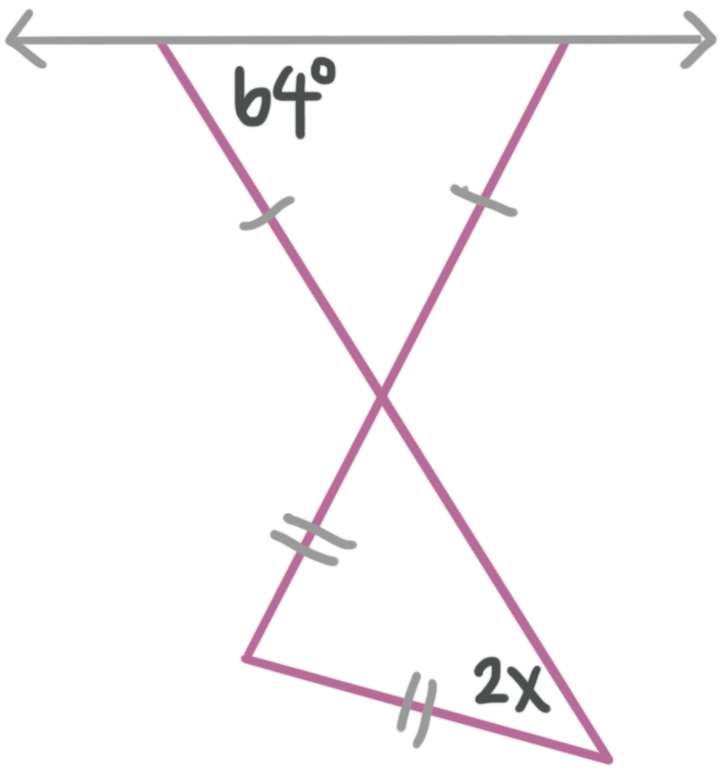
What is the value of ???x????
Let’s use what we know about isosceles triangles to fill in the diagram. Remember that the base angles of an isosceles triangle are congruent.
We also know that vertical angles are congruent, so we can fill in one more angle.
Now we can use the top triangle to solve for the variable by remembering that the interior angles in a triangle sum to ???180{}^\circ???.
???64{}^\circ +64{}^\circ +2x{}^\circ =180{}^\circ???
???128{}^\circ +2x{}^\circ =180{}^\circ???
???2x=52{}^\circ???
???x=26{}^\circ???