How to use the Vertical line test
What is the Vertical Line Test?
All functions are equations, but not all equations are functions. Functions are equations that pass the Vertical Line Test. In other words, in order for a graph to be a function, no perfectly vertical line can cross its graph more than once.
When you draw vertical lines across your graph to test it, make sure that you draw your vertical lines perfectly straight.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The graph below doesn't pass the Vertical Line Test, because a vertical line intersects it more than once. It takes only one vertical line intersecting the graph more than once for it to fail the Vertical Line Test.
Passing the Vertical Line Test also implies that the graph has only one output ???y??? for any input ???x???. You know that a relation is not a function if there is at least one value of ???x??? that’s related to two different values of ???y???.
To test for functions, we need to make sure that there’s only one ???y???-value for every ???x???-value. Visually, when you look at the graph of a relation, you can see whether every ???x???-value is related to only one ???y???-value by using the Vertical Line Test: Any (and every possible) vertical line may intersect (cross) the graph at most once. If some vertical line crosses the graph more than once, then the graph has failed the Vertical Line Test and the relation isn’t a function.
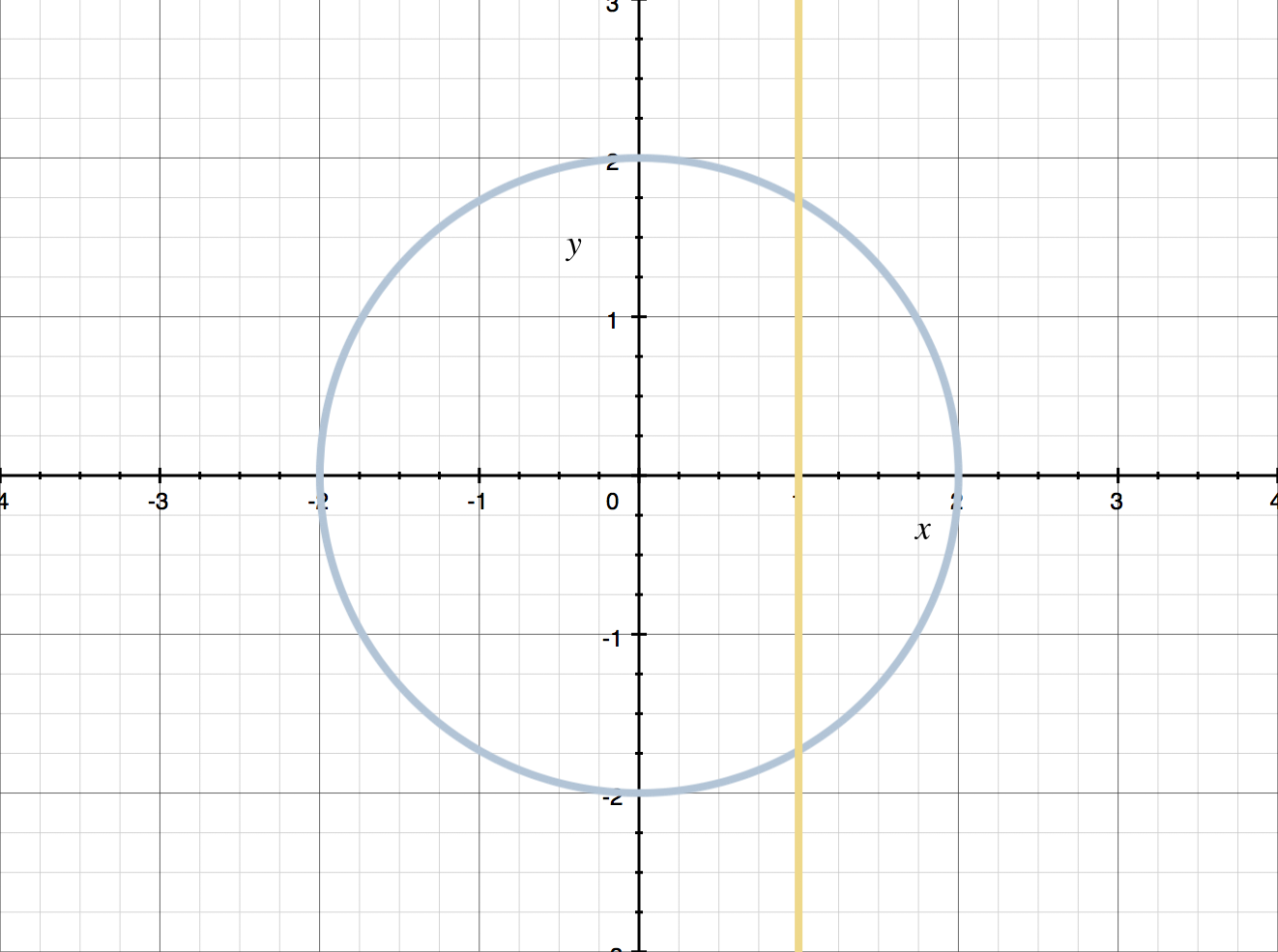
You know that the circle below doesn’t represent a function, because any vertical line you draw at some ???x??? that’s strictly between ???-2??? and ???2??? (not “right at” ???-2??? or ???2???) will cross the graph twice, which causes the graph to fail the Vertical Line Test. In fact, circles can never represent functions, because they never pass the Vertical Line Test.
How to use the Vertical Line Test to determine whether or not a graph represents a function
Take the course
Want to learn more about Algebra 1? I have a step-by-step course for that. :)
When does a graph fail the Vertical Line Test?
Example
How many times can a vertical line touch a graph in order to pass the Vertical Line Test?
Every vertical line can only touch a graph once in order for the function to pass the Vertical Line Test. If a graph passes the Vertical Line Test, it’s the graph of a function.
Let’s do an example with another equation.
Every vertical line can only touch a graph once in order for the function to pass the Vertical Line Test. If a graph passes the Vertical Line Test, it’s the graph of a function.
Example
Determine algebraically whether or not the equation represents a function.
???x^2+y^2=1???
Plug in ???0??? for ???x??? and simplify.
???(0)^2+y^2=1???
???y^2=1???
Now take the square root of each side.
???\sqrt{y^2}=\sqrt{1}???
???y=\pm 1???
Looking at it another way, at ???x=0??? , ???y??? can be both ???1??? and ???-1??? . Since a function can only have one unique output value for ???y??? for any input value of ???x???, the function fails the Vertical Line Test and is therefore not a function. We’ve now proven with both the graph and with algebra that this circle is not a function.