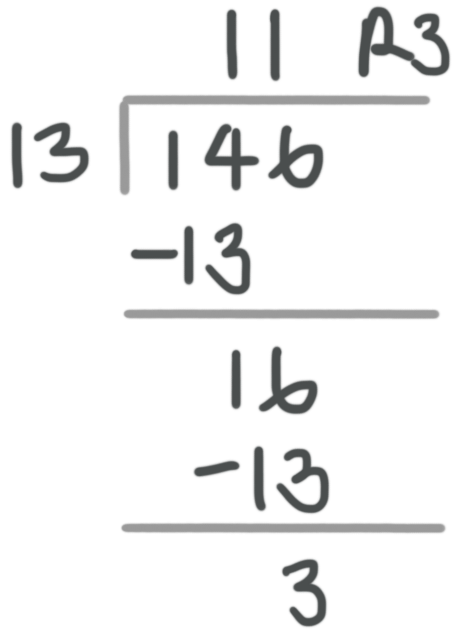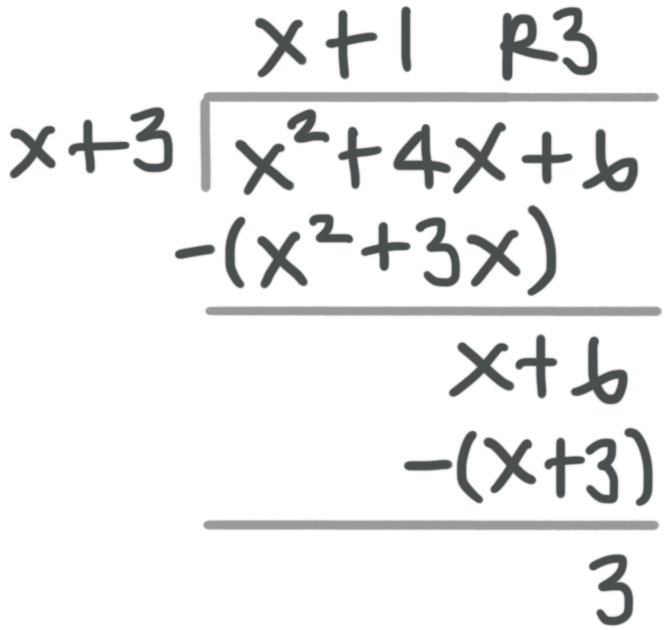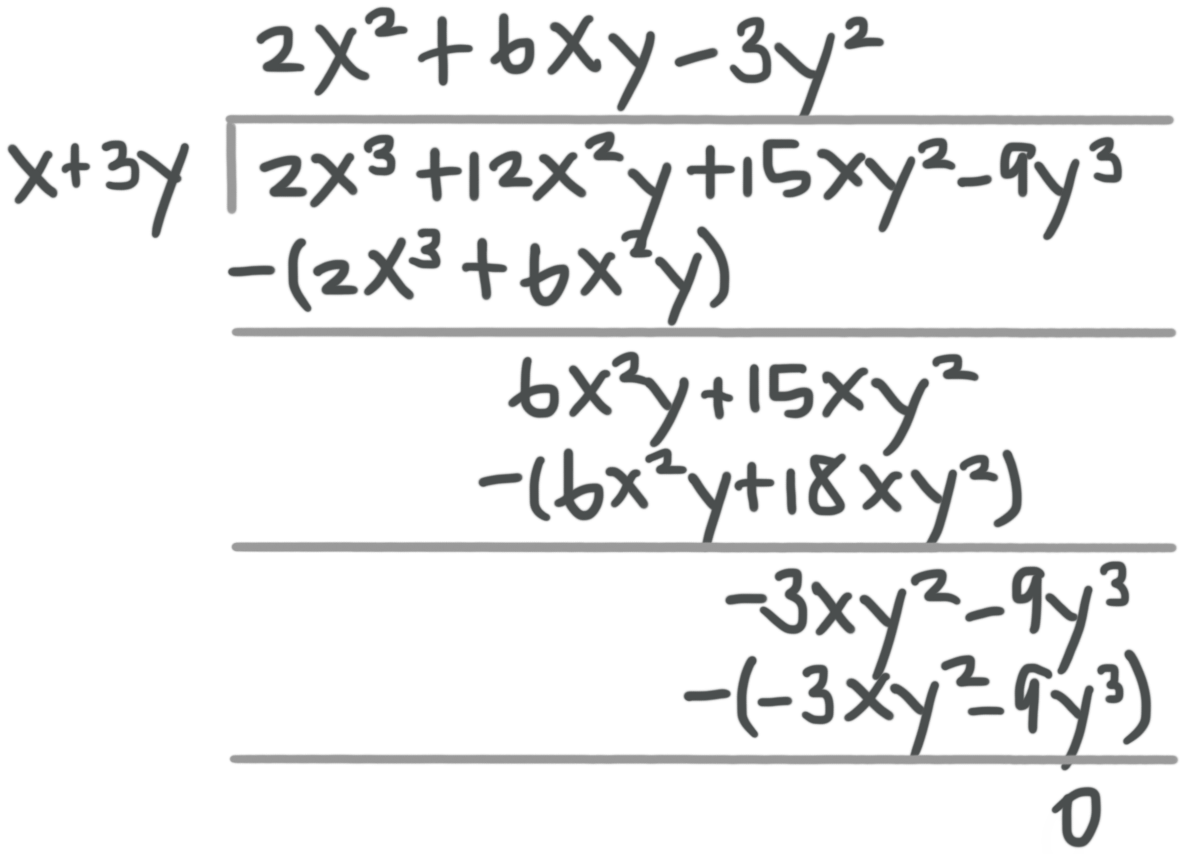How to do polynomial long division with multivariable polynomials
Using polynomial long division with multiple variables
Dividing multivariable polynomials is very similar to dividing single-variable polynomials. We’ll still use long division, but now we’ll have more than one variable.
Let’s review long division by dividing ???146??? by ???13???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
We start by thinking, “How many times does ???13??? go into ???14????” It’s ???1??? time, so we write a ???1??? above the long division sign and line it up with the ???4???.
Then we multiply ???13??? by ???1??? and get ???13???, which means we subtract ???13??? from ???14??? and get ???1???. Bring down the ???6???.
How many times does ???13??? go into ???16???? ???1??? time, so we write another ???1??? above long division sign, this time line up with the ???6???.
???13\times1=13???, which means we subtract ???13??? from ???16??? and get ???3???. Since ???13??? doesn’t go into ???3???, we have a remainder of ???3???.
Our answer to ???146\div 13??? is ???11) with a remainder of ???3???, or
???11 \frac{3}{13}???
Now let’s look at the same problem using polynomial long division. This time we’ll divide ???x^2+4x+6??? by ???x+3???.
The leading term in the dividend (???x^2+4x+6???) is ???x^2???, and the leading term in the divisor (???x+3???) is ???x???. So we start by thinking, “What do I need to multiply ???x??? by to get ???x^2????” The answer is ???x???, so we write ???x??? above the long division sign and line it up with the ???x^2???.
Then we multiply ???x+3??? by ???x??? and get ???x^2+3x???, which means we subtract ???x^2+3x??? from ???x^2+4x??? and get ???x???. Bring down the ???+6???.
What do we need to multiply ???x??? by in order to get ???x???? The answer is ???1???, so we write ???+1??? next to the ???x??? above the long division sign.
???(x+3)\cdot1=x+3???, so subtract ???x+3??? from ???x+6??? and get ???3???.
Our answer is ???x+1??? with a remainder of ???3???. When we do polynomial long division, we should write the remainder as a fraction, with the remainder in the numerator and the divisor in the denominator, so the answer can be written as
???x+1+\frac{3}{x+3}???
Remember to always have placeholders for any “missing” terms (terms that have a coefficient of ???0???) in the dividend. For example, if the problem above hadn’t had an ???x??? term, we would have needed to write ???x^2+0x+6??? under the long division sign.
Several examples of long division with multivariable polynomials
Take the course
Want to learn more about Algebra 1? I have a step-by-step course for that. :)
How to divide multivariable polynomials
Example
Find the quotient.
???\frac{x^3+2x^2y-y^3}{x+y}???
We’ll use polynomial long division to find the quotient. Remember to put in ???+0xy^2??? as a placeholder.
Let’s try another example of dividing multivariable polynomials.
Dividing multivariable polynomials is very similar to dividing single-variable polynomials. We’ll still use long division, but now we’ll have more than one variable.
Example
Find the quotient.
???\frac{2x^3+12x^2y+15xy^2-9y^3}{x+3y}???
We’ll use polynomial long division to find the quotient.