System of two equations with a non-linear equation
How to approach solving a system of equations where one equation isn’t linear
This lesson will show you the algebraic way of solving a pair of equations where one is a linear equation, which is the equation of a line where all variables are first-degree variables, like ???x??? and ???y???. The other equation will have at least one squared variable in it, like ???x^2??? or ???y^2???.
In a system, all equations will have the same or overlapping unknowns. If you have a pair of equations with two variables, there are a variety of ways to solve for the values of the unknowns that make both equations true.
Remember:
An equation for a circle or an ellipse has both an ???x^2??? term and a ???y^2??? term. It might look like ???x^2+4y^2=100???.
An equation for a line has an ???x??? and a ???y??? term with no written exponents. An example of a linear equation would be ???y=-(3/2)x-5???.
If you take the two equations and put them together,
???\begin{cases}x^2+4y^2=100 \\y=-\frac{3}{2}x-5 \end{cases}???
then you have a system of equations.
The solutions to a system of equations are where the graphs of both equations intersect each other. Let’s look at how to solve this system in the next example.
Solving the system when one equation is linear and the other is quadratic
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. :)
An example of solving a system of two equations with a quadratic equation and a linear equation
Example
Solve the system for ???x??? and ???y???.
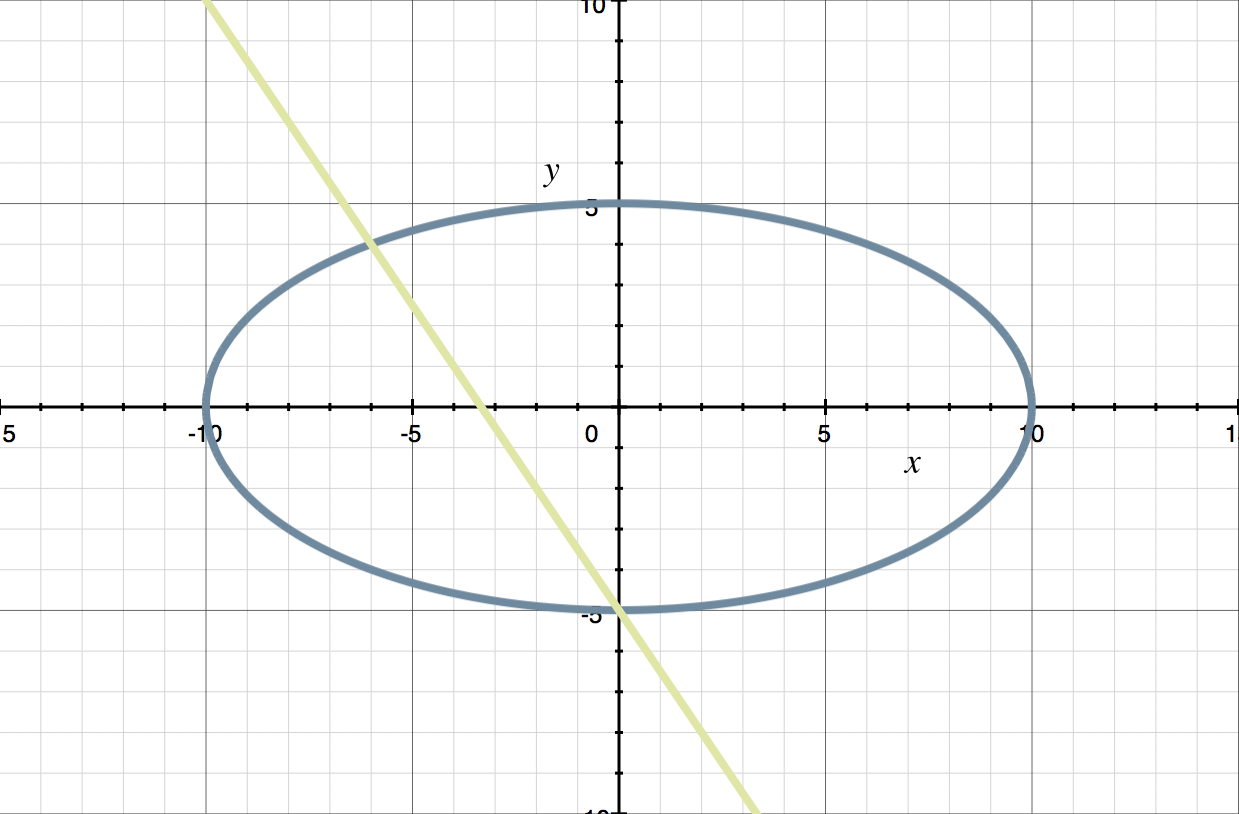
???\begin{cases}x^2+4y^2=100 \\y=-\frac{3}{2}x-5 \end{cases}???
In this case the second equation is already solved for ???y???, so we can begin by substituting this value for ???y??? into the first equation.
???x^2+4y^2=100???
???x^2+4\left(-\frac{3}{2}x-5\right)^2=100???
Expand the square.
???x^2+4\left(-\frac{3}{2}x-5\right)\left(-\frac{3}{2}x-5\right)=100???
???x^2+4\left(\frac{9}{4}x^2+15x+25\right)=100???
Distribute the ???4??? across everything inside the parentheses.
???x^2+9x^2+60x+100=100???
???x^2+9x^2+60x+100-100=0???
???10x^2+60x=0???
Factor out a ???10x??? to help solve for ???x???.
???10x(x+6)=0???
???10x=0??? and ???x+6=0???
???x=0??? and ???x=-6???
Plug these ???x???-values into ???y=-(3/2)x-5??? to find the ???y???-values that go with them.
When ???x=0???,
???y=-\frac{3}{2}(0)-5=-5???
so we have the solution ???(0,-5)???. And when ???x=-6???,
???y=-\frac{3}{2}(-6)-5=4???
so we have the solution ???(-6,4)???.
You can look at this picture of the system to see that the solutions are where the ellipse and line intersect.
Let’s do another example that involves a few more steps.
Example
Solve the system for ???x??? and ???y???.
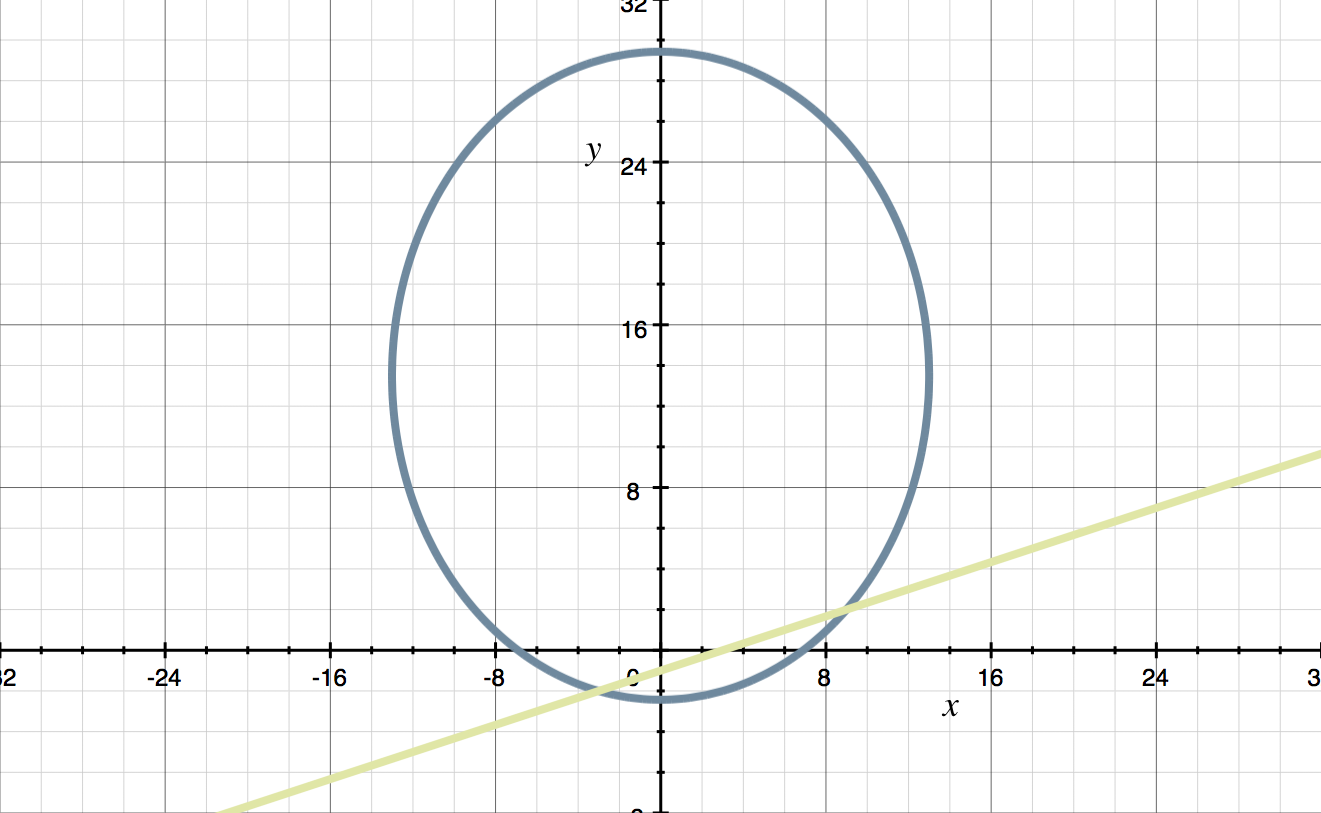
???3x^2+2y^2-54y=143???
???x-3y=3???
Solving a system means we’re finding where the graphs of the two equations intersect each other.
Let’s solve this system by solving the second equation for ???y??? and then making a substitution for ???y??? into the first equation.
???x-3y=3???
???-3y=-x+3???
???\frac{-3}{-3}y=\frac{-x}{-3}+\frac{3}{-3}???
???y=\frac{1}{3}x-1???
Plug this value for ???y??? into the first equation and then solve for ???x???.
???3x^2+2y^2-54y=143???
???3x^2+2\left(\frac{1}{3}x-1\right)^2-54\left(\frac{1}{3}x-1\right)=143???
Expand the square.
???3x^2+2\left(\frac{1}{3}x-1\right)\left(\frac{1}{3}x-1\right)-54\left(\frac{1}{3}x-1\right)=143???
???3x^2+2\left(\frac{1}{9}x^2-\frac{2}{3}x+1\right)-18x+54=143???
???3x^2+\frac{2}{9}x^2-\frac{4}{3}x+2-18x+54=143???
Combine like terms.
???3x^2+\frac{2}{9}x^2-\frac{4}{3}x-18x+54 +2-143=0???
???\frac{29}{9}x^2- \frac{58}{3}x- 87= 0???
Clear fractions by multiplying through by ???9???.
???9\left(\frac{29}{9}x^2- \frac{58}{3}x- 87\right)= 9\cdot0???
???9\cdot \frac{29}{9}x^2-9 \cdot \frac{58}{3}x-9\cdot 87=0???
???29x^2-174x-783=0???
We can simplify more by dividing everything by ???29???.
???\frac{29}{29}x^2-\frac{174}{29}x-\frac{783}{29}=\frac{0}{29}???
???x^2-6x-27=0???
Factor, then solve for ???x???.
???(x-9)(x+3)=0???
???x-9=0??? and ???x+3=0???
???x=9??? and ???x=-3???
Plug these values for ???x??? into the equation you solved for ???y??? to find their corresponding ???y???-values.
???y=\frac{1}{3}x-1???
???y=\frac{1}{3}(9)-1=2???
So one solution is ???(9,2)???, and
???y=\frac{1}{3}(-3)-1=-2???
the other is ???(-3,-2)???.
Sometimes it’s nice to have a visual of what we just did. Here’s a graph of the ellipse and the line. Notice that they intersect at the solution points ???(-3,-2)??? and ???(9,2)???.