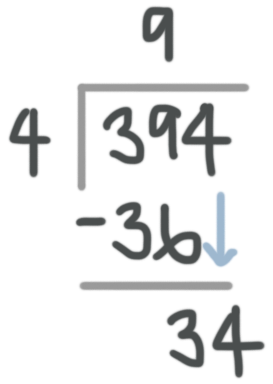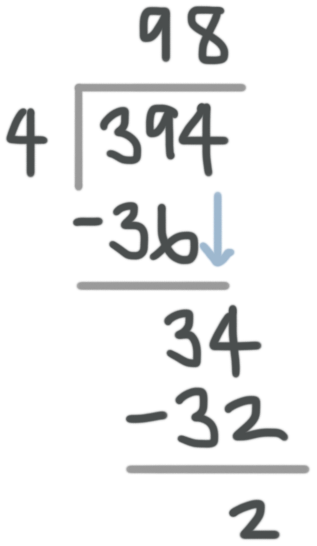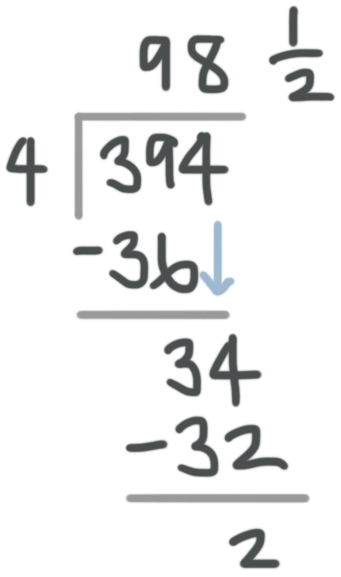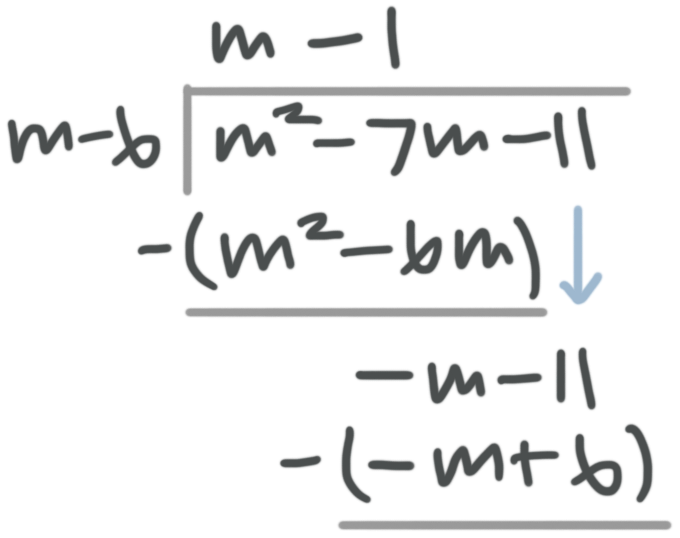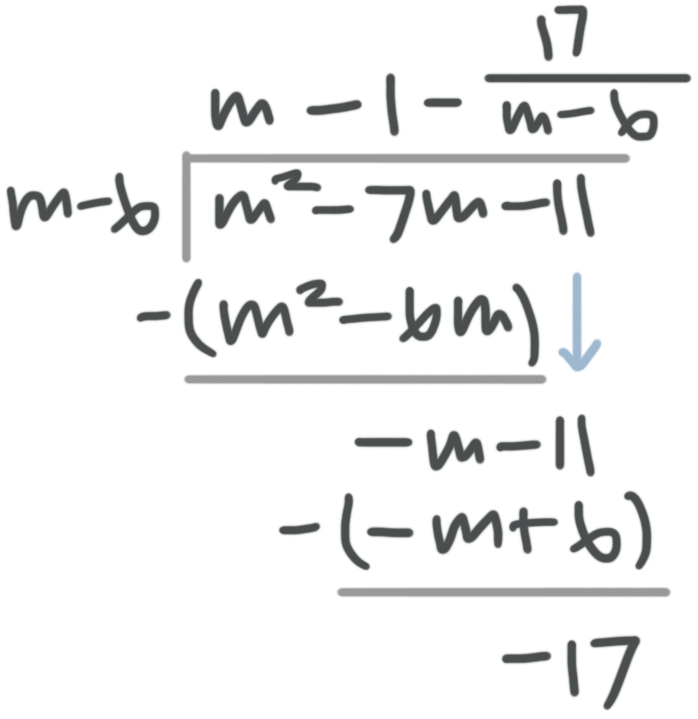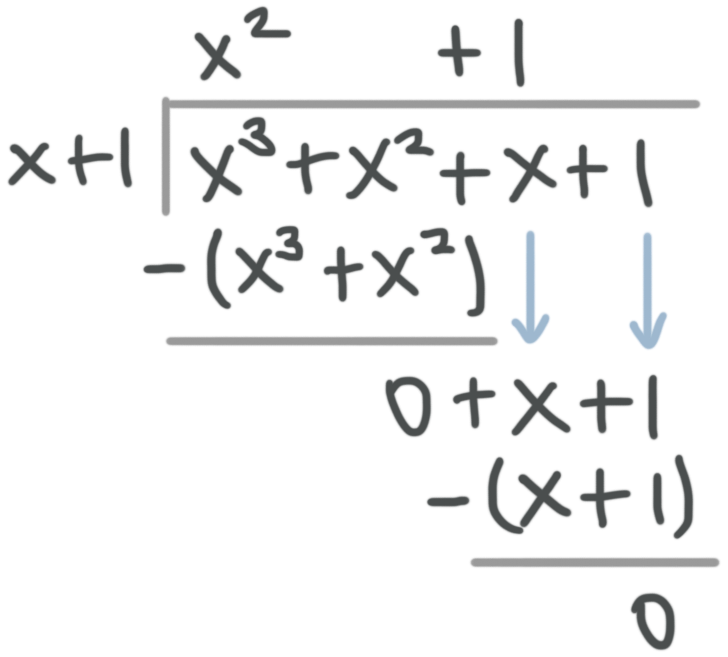How to do long division with polynomials
The steps to follow to perform polynomial long division
Long division of polynomials uses the same steps you learned for long division of real numbers.
It might look different because of the variables but don’t worry, it’s the same thing in disguise.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Let’s first review long division.
Remember this? You followed a pattern of Divide, Multiply, Subtract, Bring Down.
Here ???4??? is bigger than ???3??? so you need to start with the tens place.
Now think, ???4??? times ???9??? is ???36???, write the ???9??? above the ten’s place and the ???36??? under ???3??? and ???9??? in the division problem then subtract and bring down the ???4???.
Now ???9??? is too big but ???4??? times ???8??? is ???32???, so write the ???8??? above the ones place and the ???32??? under the ???3??? and ???4??? in the division problem then subtract.
The ???2??? is the remainder so write it as a fraction ???2/4??? or ???1/2???.
This is the same technique you use for polynomials. Let’s check it out.
How to do polynomial long division
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. :)
A couple of examples of long division of polynomials
Example
Find the quotient.
???\frac{m^2-7m-11}{m-6}???
First set it up as a division problem.
Now divide ???m^2??? by ???m??? to get ???m???. This means we need to multiply ???m-6??? by ???m???.
???m(m-6)=m^2 - 6m???
Write the ???m??? above the ???7m??? in the division problem and the ???m^2-6m??? under the ???m^2 - 7m???.
Remember, you’re subtracting next.
Now divide ???-m??? by ???m???, which is ???-1.???
???-1(m-6)=-m+6???
Write the ???-1??? above the ???-11??? in the division problem and the ???-m+6??? under the ???-m-11???.
Remember you need to subtract.
Now write the integer term as the remainder or fractional part.
Let’s do another example.
You followed a pattern of Divide, Multiply, Subtract, Bring Down.
Example
Use long division to simplify the rational function.
???f(x)=\frac{x^3+x^2+x+1}{x+1}???
First, we should keep in mind that the divisor is ???x+1??? and the dividend is ???x^3+x^2+x+1???.
To start our long division problem, we determine what we have to multiply by ???x??? (in the divisor) to get ???x^3??? (in the dividend). Since the answer is ???x^2???, we put that on top of our long division problem, and multiply it by the divisor, ???x+1???, to get ???x^3+x^2???, which we then subtract from the dividend.
We bring down ???x??? from the dividend and repeat the same steps until we have nothing left to carry down from the dividend. Our original problem reduces to:
???f(x)=x^2+1???