Solving for measures of angles
What is an angle, and how do we measure it?
In this lesson we’ll look at how to find the measures of angles, in degrees, algebraically.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The measure of angles
An angle is a fraction of a circle, the turn of the angle is measured in degrees (or radians).
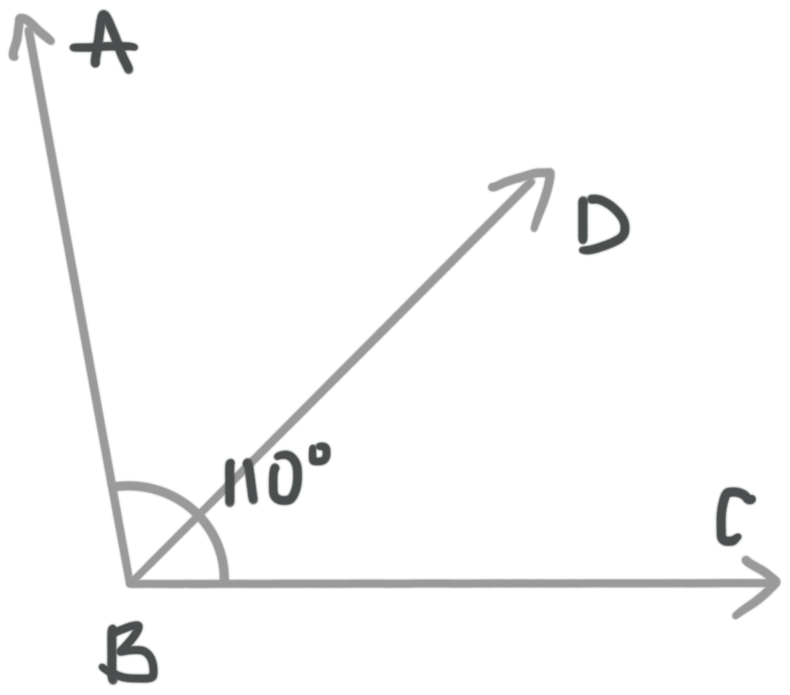
The name of this angle is ???\angle ABC???. When we talk about the measure of the angle we use an ???m??? in front of the angle sign, ???m\angle ABC=110{}^\circ???.
Angle addition
The parts of an angle add to the entire angle.
Here you can see that ???m\angle ABC=m\angle ABD+m\angle DBC???. This means if you know ???m\angle DBC=55{}^\circ??? and ???m\angle ABC=110{}^\circ??? you can find ???m\angle ABD???.
???m\angle ABC=m\angle ABD+m\angle DBC???
???110{}^\circ =m\angle ABD+55{}^\circ???
???55{}^\circ =m\angle ABD???
How to add and subtract angles to find their measures
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Solving for angle measures
Example
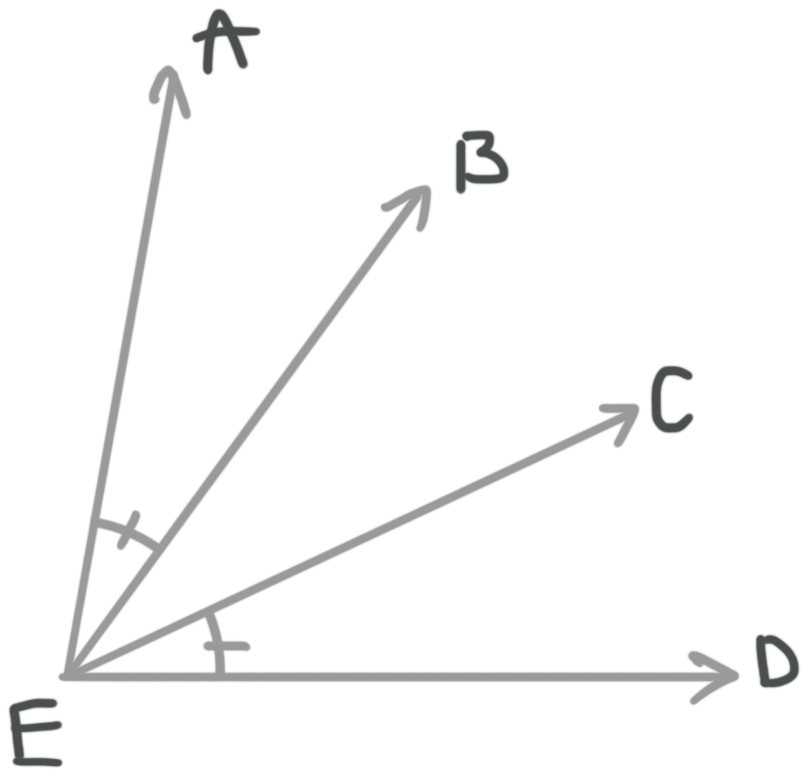
If ???m\angle AED=80{}^\circ??? and ???m\angle AEB=30{}^\circ???, what is ???m\angle BEC????
Let’s organize what we know. Looking at the diagram we can see that ???\angle AEB??? is congruent to ???\angle CED???. So we know both angles measure the same, ???m\angle AEB=m\angle CED=30{}^\circ???.
We also know the measure of the entire angle ???m\angle AED=80{}^\circ???. Also ???m\angle AED=m\angle AEB+m\angle BEC+m\angle CED???. Let’s rename ???m\angle BEC??? with the variable ???x???. Then we get
???m\angle AED=m\angle AEB+m\angle BEC+m\angle CED???
???80{}^\circ =30{}^\circ +x+30{}^\circ???
???80{}^\circ =60{}^\circ +x???
???x=20{}^\circ???
So ???m\angle BEC=20{}^\circ???.
Here’s another type of problem you might see.
An angle is a fraction of a circle, the turn of the angle is measured in degrees (or radians).
Example
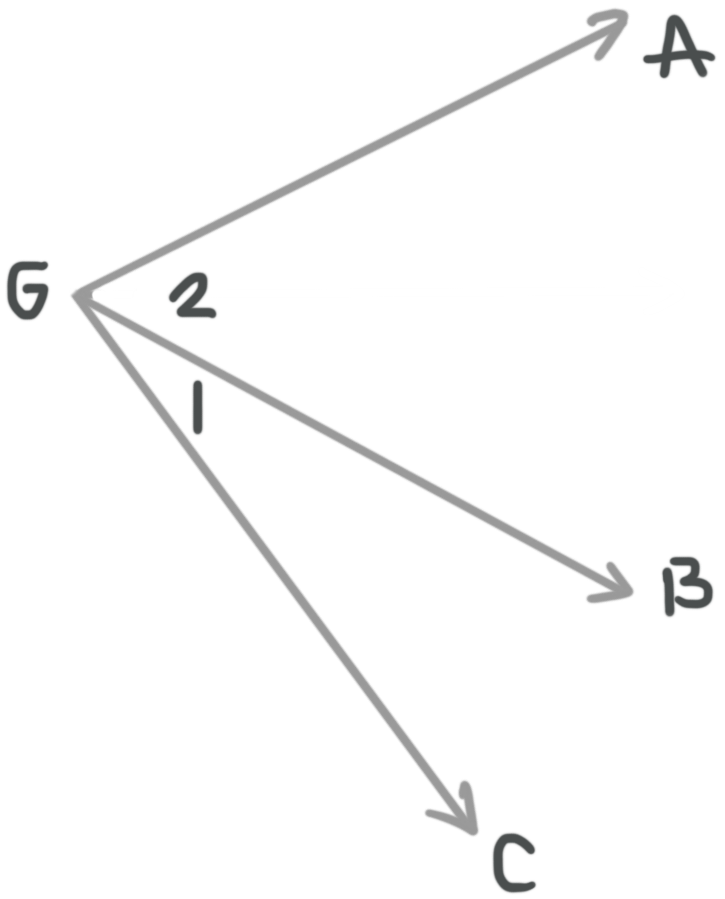
Find the angle measure of ???\angle 2??? in degrees.
???m\angle 1=2x{}^\circ???
???m\angle 2=5x{}^\circ +5{}^\circ???
???m\angle AGC=105{}^\circ -3x{}^\circ???
We can set up an equation, solve for ???x???, then substitute back in to find ???m\angle 2???.
???m\angle 1+m\angle 2=m\angle AGC???
???2x{}^\circ +5x{}^\circ +5{}^\circ =105{}^\circ -3x{}^\circ???
???7x{}^\circ +5{}^\circ =105{}^\circ -3x{}^\circ???
???7x{}^\circ +3x{}^\circ +5{}^\circ =105{}^\circ???
???10x{}^\circ +5{}^\circ =105{}^\circ???
???10x{}^\circ =100{}^\circ???
???x{}^\circ =10{}^\circ???
Substituting into ???m\angle 2=5x{}^\circ +5{}^\circ???, we get ???m\angle 2=5(10){}^\circ +5{}^\circ =55{}^\circ???.