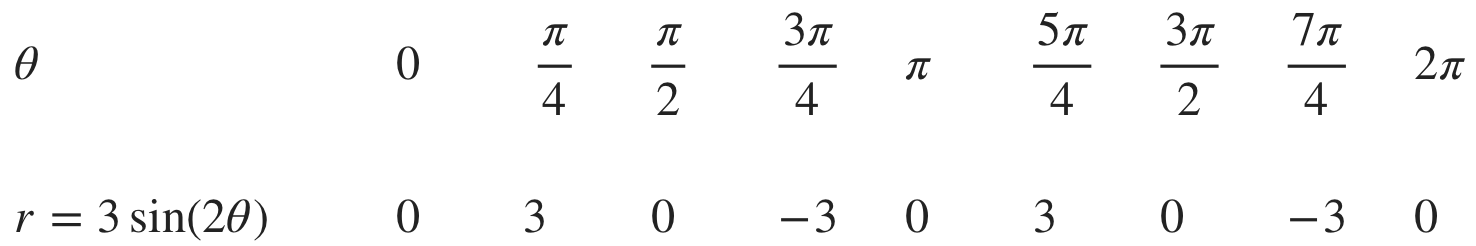Finding the area bounded by one loop of a polar curve
The formula we use to find the area inside the polar curve
When we need to find the area bounded by a single loop of the polar curve, we’ll use the same formula we used to find area inside the polar curve in general.
???A=\int^{\beta}_{\alpha}\frac12r^2\ d\theta???
where ???[\alpha,\beta]??? is the interval
where ???r??? is the equation of the polar curve
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The best way to find the interval that defines one loop of the curve is to graph the curve.
How to find the area bounded by one loop of a polar curve
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Finding the area bounded by one loop of the graph of a polar curve
Example
Find the area bounded by one loop of the the polar curve.
???r=3\sin{(2\theta)}???
We’ll start by finding points that we can use to graph the curve. In order to do so, we’ll take the value inside the trigonometric function, set it equal to ???\pi/2???, and solve for ???\theta???.
???2\theta=\frac{\pi}{2}???
???\theta=\frac{\pi}{4}???
We need to find coordinate points for multiples of ???\pi/4??? in the interval ???0\leq\theta\leq2\pi???.
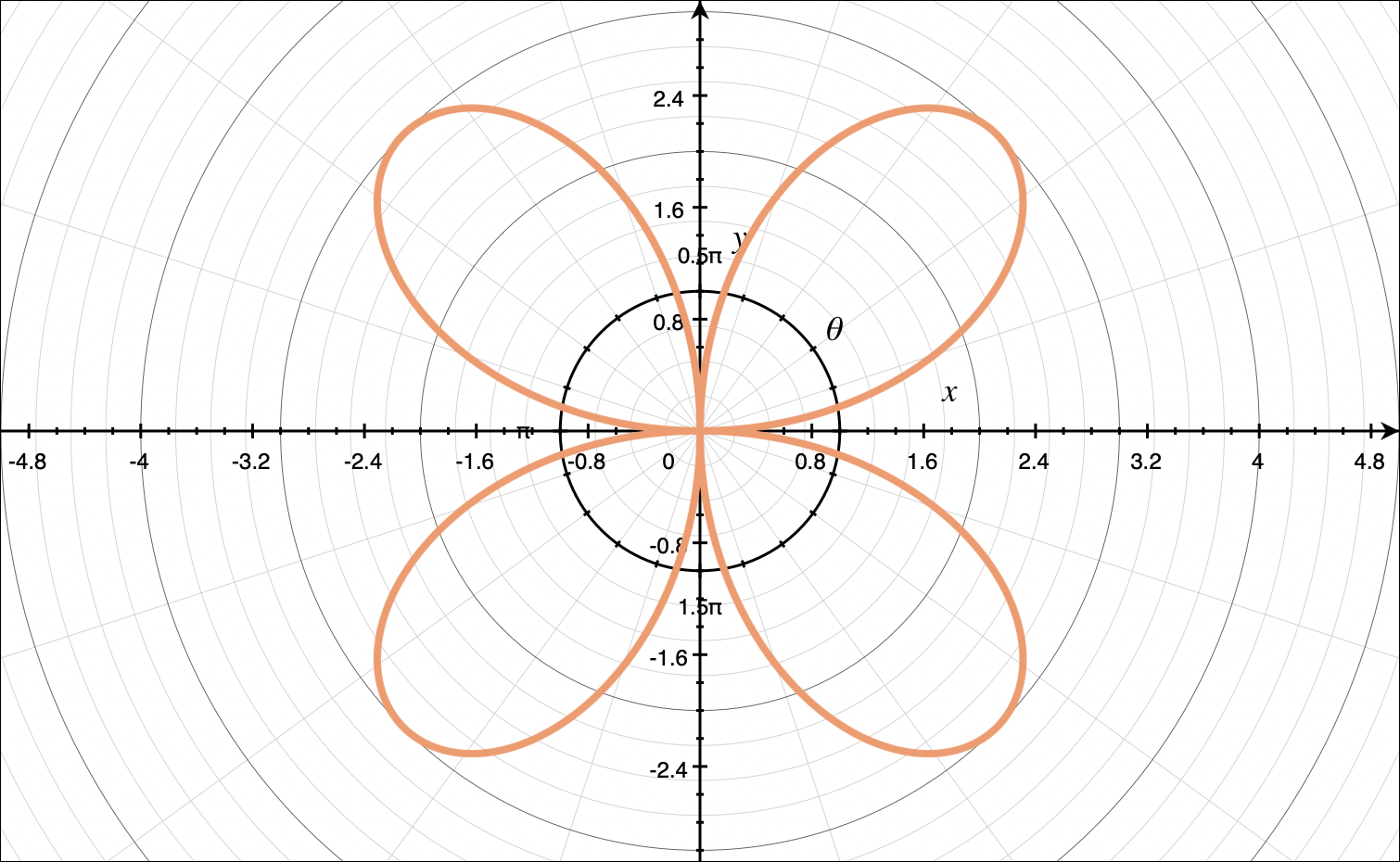
Plotting these points on polar axes, we get
From the graph, we can see that the curve starts at ???(0,0)???, goes out to ???3??? at an angle ???\pi/4???, then curves back to the origin at the angle ???\pi/2???. Plugging this into the area formula, we get
???A=\int^{\frac{\pi}{2}}_{0}\frac12\left[3\sin{(2\theta)}\right]^2\ d\theta???
???A=\int^{\frac{\pi}{2}}_{0}\frac12\left[9\sin^2{(2\theta)}\right]\ d\theta???
???A=\frac92\int^{\frac{\pi}{2}}_{0}\sin^2{(2\theta)}\ d\theta???
When we need to find the area bounded by a single loop of the polar curve, we’ll use the same formula we used to find area inside the polar curve in general.
We’ll use u-substitution, letting
???u=2\theta???
???du=2\ d\theta???
???d\theta=\frac{du}{2}???
We’ll substitute into the integral.
???A=\frac92\int^{\theta=\frac{\pi}{2}}_{\theta=0}\sin^2{u}\ \frac{du}{2}???
???A=\frac94\int^{\theta=\frac{\pi}{2}}_{\theta=0}\sin^2{u}\ du???
Since ???\sin^2{u}=\frac12\left[1-\cos{(2u)}\right]???, we get
???A=\frac94\int^{\theta=\frac{\pi}{2}}_{\theta=0}\frac12\left[1-\cos{(2u)}\right]\ du???
???A=\frac94\int^{\theta=\frac{\pi}{2}}_{\theta=0}\frac12-\frac{1}{2}\cos{(2u)}\ du???
???A=\frac94\left[\frac12u-\frac14\sin{(2u)}\right]\bigg|^{\theta=\frac{\pi}{2}}_{\theta=0}???
Back-substituting for ???u???, we get
???A=\frac94\left[\frac12(2\theta)-\frac14\sin{(2(2\theta))}\right]\bigg|^{\frac{\pi}{2}}_{0}???
???A=\frac94\left[\theta-\frac14\sin{(4\theta)}\right]\bigg|^{\frac{\pi}{2}}_{0}???
???A=\frac94\left[\frac{\pi}{2}-\frac14\sin{\left(4\cdot\frac{\pi}{2}\right)}-\left(0-\frac14\sin{(4\cdot0)}\right)\right]???
???A=\frac94\left(\frac{\pi}{2}-\frac{1}{4}\sin{2\pi}+\frac14\sin{0}\right)???
???A=\frac94\left(\frac{\pi}{2}-\frac14(0)+\frac14(0)\right)???
???A=\frac94\left(\frac{\pi}{2}\right)???
???A=\frac{9\pi}{8}???