Finding the inverse of a function
How to define inverse functions
In this lesson we’ll look at the definition of an inverse function and how to find a function’s inverse.
If you remember from the last lesson, a function is invertible (has an inverse) if it’s one-to-one. Now let’s look a little more into how to find an inverse and what an inverse does.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
When you have a function with points ???(x, f(x))???, the inverse function will have points ???(f(x), x)???. The inverse of a function ???f(x)??? is written as ???f^{-1}(x)???.
For example, if ???g(x)??? and ???g^{-1}(x)??? are inverses of one another, then the tables below would give sets of points from each,
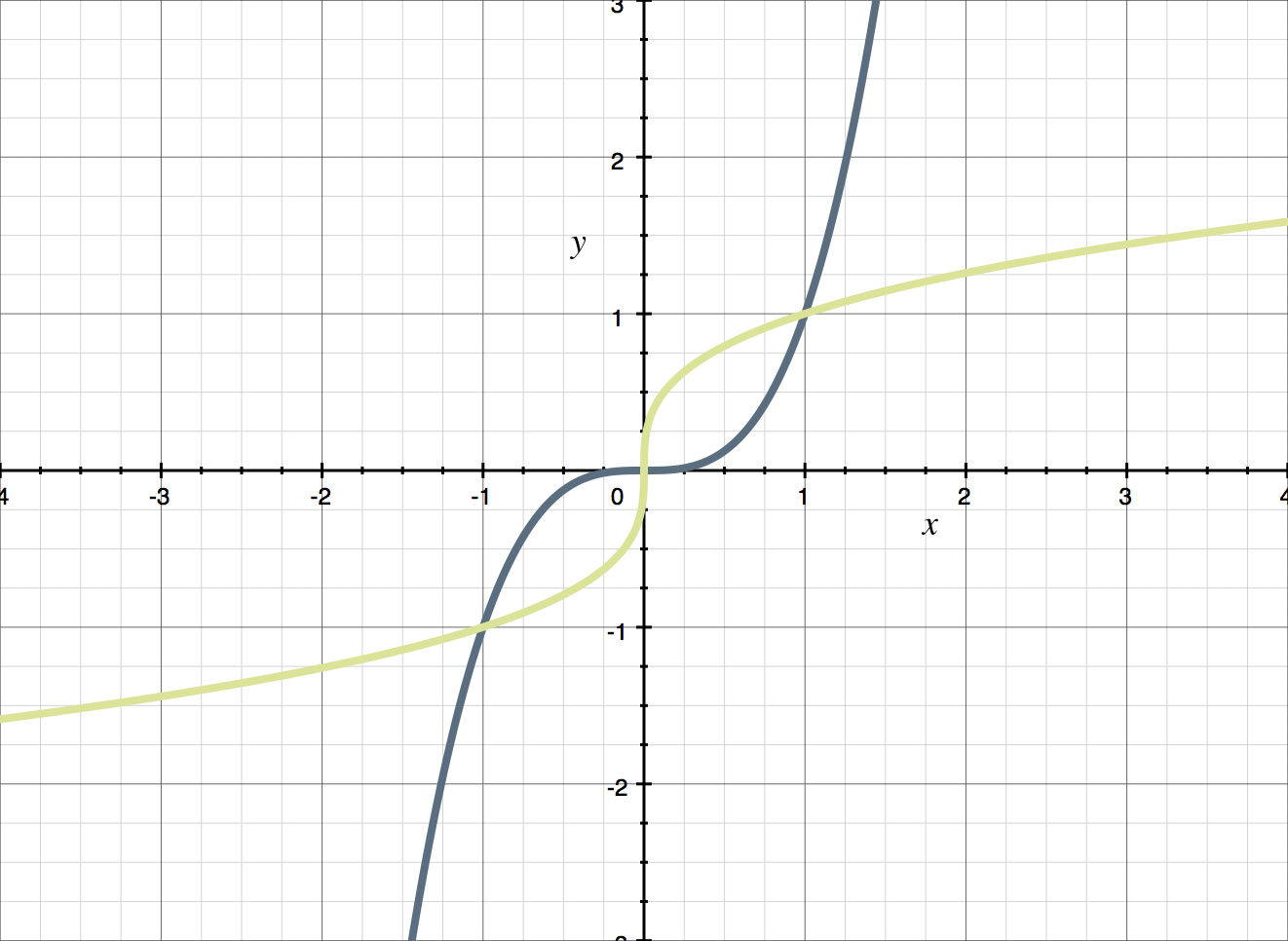
Now let’s look at the graphs of a function and its inverse. Look at the graph of the function ???f(x)=x^3??? and its inverse ???f^{-1}(x)= \sqrt[3]{x}???.
???x=(x^3)^\frac13=\sqrt[3]{x^3}???
Notice how the coordinates of the ???x??? and ???y???-values have switched places. Now let’s look at how to calculate an inverse algebraically.
Calculating and graphing inverse functions
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. :)
Finding the inverse of a given function
Example
What is the inverse of the function?
???f(x)=\frac{2}{3}x-4???
First, remember the function is invertible because non-horizontal linear functions are one-to-one.
To find an inverse, first rewrite ???f(x)??? with the variable ???y???.
???y=\frac{2}{3}x-4???
Now switch the ???x??? and ???y??? values.
???x=\frac{2}{3}y-4???
Now solve for ???y???.
???\frac{3}{2} \cdot x+\frac{3}{2} \cdot 4=\frac{3}{2} \cdot \frac{2}{3}y???
???\frac{3}{2}x+6=y???
Now you can write the inverse function.
???f^{-1}(x)= \frac{3}{2}x+6???
Let’s do one more example.
When you have a function with points (x, f(x)), the inverse function will have points (f(x), x).
Example
Find the inverse of the function.
???g(x)=\frac{x}{x-3}???
First replace ???g(x)??? with ???y???.
???y=\frac{x}{x-3}???
Now switch the ???x??? and ???y??? values and solve for ???y???.
???x=\frac{y}{y-3}???
???x(y-3)=y???
???xy-3x=y???
???xy-y=3x???
???y(x-1)=3x???
???y=\frac{3x}{x-1}???
The inverse function is
???g^{-1}(x) =\frac{3x}{x-1}???