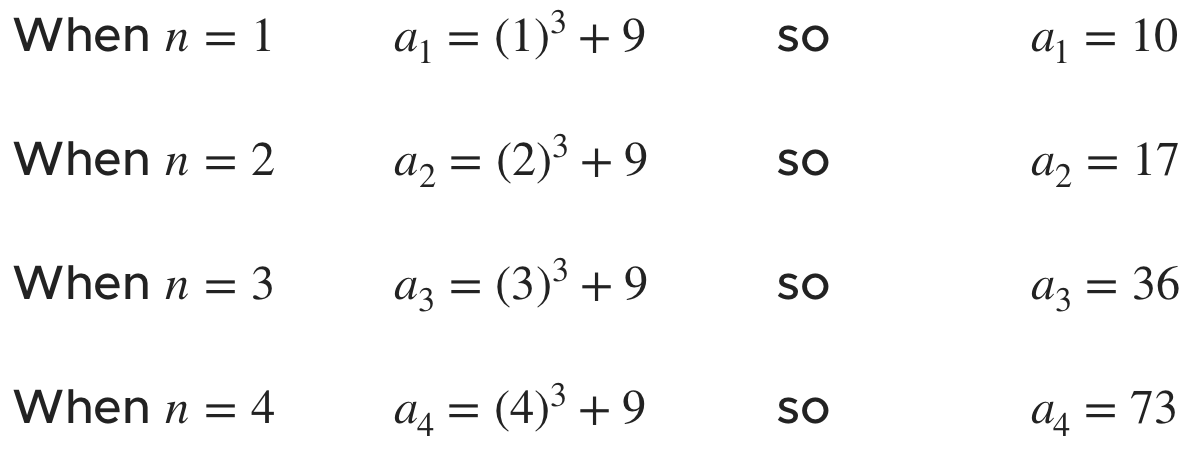Determining whether a series is increasing, decreasing, or not monotonic
What does it mean for a series to be increasing, decreasing, or not monotonic?
Sequences are always either monotonic or not monotonic. If a sequence is monotonic, it means that it’s always increasing or always decreasing.
If a sequence is sometimes increasing and sometimes decreasing and therefore doesn’t have a consistent direction, it means that the sequence is not monotonic.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
In other words, a non-monotonic sequence is increasing for parts of the sequence and decreasing for others.
The fastest way to make a guess about the behavior of a sequence is to calculate the first few terms of the sequence and visually determine if it’s increasing, decreasing or not monotonic.
If we want to get more technical and prove the behavior of the sequence, we can use the following inequalities.
A sequence is increasing if ???a_n\le{a_{n+1}}???
A sequence is decreasing if ???a_n\ge{a_{n+1}}???
A sequence is not monotonic if ???a_n\le{a_{n+1}}\ge{a_{n+2}}??? or ???a_n\ge{a_{n+1}}\le{a_{n+2}}???.
How to determine whether or not a series is monotonic, and if it is monotonic, whether its increasing or decreasing
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
A step-by-step example of determining whether or not a sequence is monotonic
Example
Is the sequence increasing, decreasing or not monotonic?
???a_n=n^3+9???
We can start by determining the first few values of the sequence. Let’s calculate ???n=1???, ???n=2???, ???n=3??? and ???n=4???.
If a sequence is sometimes increasing and sometimes decreasing and therefore doesn’t have a consistent direction, it means that the sequence is not monotonic.
The first four terms of our sequence are ???\left\{10,\ 17,\ 36,\ 73\right\}???. Looking at these first few terms, we can see that the sequence is increasing. If we want to be more strict, we can prove it by showing that ???a_n\le{a_{n+1}}???.
???n^3+9\le{(n+1)^3+9}???
???n^3+9\le{n^3+3n^2+3n+10}???
Looking at our inequality we can see that ???a_n\le{a_{n+1}}??? is true for our sequence. After all, ???n^3+10??? on its own has to be greater than or equal to ???n^3+9???, and adding ???3n^2+3n??? will definitely make it greater, so we know for sure that
???n^3+9\le{\left(n^3+10\right)+3n^2+3n}???
If we’re still unsure, we can always plug in a few values of ???n??? to confirm our conclusion.
The sequence ???a_n=n^3+9??? is increasing, which means it’s also monotonic.