Using Green's Theorem to evaluate a line integral in two regions
What is Green’s Theorem?
Green’s theorem gives us a way to change a line integral into a double integral.
If a line integral is particularly difficult to evaluate, then using Green’s theorem to change it to a double integral might be a good way to approach the problem.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
If we want to find the area of a region which is the union of two simple regions, and the original line integral has the form
???\oint_cP\ dx+Q\ dy???
then we can apply Green’s theorem to change the line integral into a double integral in the form
???\int\int_{R_1}\left(\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}}\right)\ dA+\int\int_{R_2}\left(\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}}\right)\ dA???
where
???\frac{\partial{Q}}{\partial{x}}??? is the partial derivative of ???Q??? with respect to ???x???
???\frac{\partial{P}}{\partial{y}}??? is the partial derivative of ???P??? with respect to ???y???
If we choose to use Green’s theorem and change the line integral to a double integral, we’ll need to find limits of integration for both ???x??? and ???y??? so that we can evaluate the double integral as an iterated integral. Often the limits for ???x??? and ???y??? will be given to us in the problem.
How to use Green’s Theorem to find the line integral
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Using Green’s Theorem to evaluate a line integral
Example
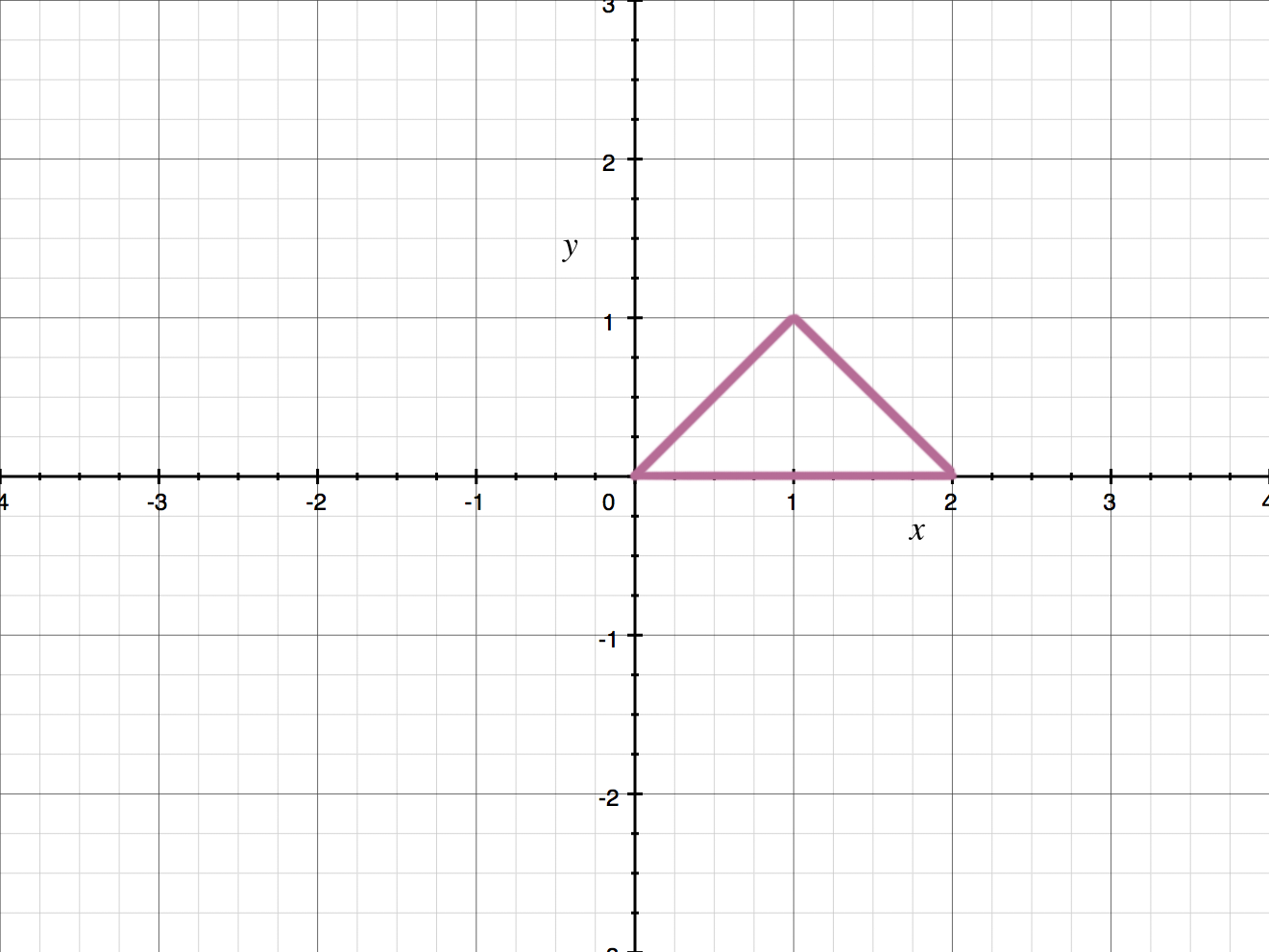
Solve the line integral for the triangular region with vertices at ???(0,0)???, ???(1,1)??? and ???(2,0)???.
???\oint_c\left(5\sin{x}+5y\right)\ dx+\left(5x^2-3y^2\right)\ dy???
Since the integral we were given matches the form
???\oint_cP\ dx+Q\ dy???
we know we can use Green’s theorem to change it to
???\int\int_{R_1}\left(\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}}\right)\ dA+\int\int_{R_2}\left(\frac{\partial{Q}}{\partial{x}}-\frac{\partial{P}}{\partial{y}}\right)\ dA???
We’ll start by finding partial derivatives.
Since ???Q(x,y)=5x^2-3y^2???,
???\frac{\partial{Q}}{\partial{x}}=10x???
Since ???P(x,y)=5\sin{x}+5y???,
???\frac{\partial{P}}{\partial{y}}=5???
Now we just need to sketch the region so that we can find limits of integration.
Since the line connecting ???(0,0)??? and ???(1,1)??? is a different function than the line connecting ???(1,1)??? and ???(2,0)???, we’ll need to divide the region into two parts, separated by the line ???x=1???.
If we choose to use Green’s theorem and change the line integral to a double integral, we’ll need to find limits of integration for both x and y so that we can evaluate the double integral as an iterated integral.
Looking at the sketch of the region, we can say that the region on the left is defined for ???x??? on ???[0,1]??? and the region on the right is defined for ???x??? on ???[1,2]???. To find the interval for ???y??? for each region, we’ll have to find the equation of the lines connecting the points. The equation of the line connecting ???(0,0)??? and ???(1,1)??? is ???y=x???. The equation of the line connecting ???(1,1)??? and ???(2,0)??? is ???y=-x+2???. Therefore, the equation for area is
???\int_0^1\int_0^x10x-5\ dy\ dx+\int_1^2\int_0^{-x+2}10x-5\ dy\ dx???
Now we’ll integrate both double integrals with respect to ???y??? and evaluate over the associated intervals.
???\int_0^110xy-5y\Big|_{y=0}^{y=x}\ dx+\int_1^210xy-5y\Big|_{y=0}^{y=-x+2}\ dx???
???\int_0^110x^2-5x-\left[10x(0)-5(0)\right]\ dx???
???+\int_1^210x(-x+2)-5(-x+2)-\left[10x(0)-5(0)\right]\ dx???
???\int_0^110x^2-5x\ dx+\int_1^2-10x^2+20x+5x-10\ dx???
???\int_0^110x^2-5x\ dx+\int_1^2-10x^2+25x-10\ dx???
Now we’ll integrate with respect to ???x??? and evaluate over each interval.
???\frac{10}{3}x^3-\frac52x^2\Big|_0^1-\frac{10}{3}x^3+\frac{25}{2}x^2-10x\Big|_1^2???
???\frac{10}{3}(1)^3-\frac52(1)^2-\left[\frac{10}{3}(0)^3-\frac52(0)^2\right]???
???-\frac{10}{3}(2)^3+\frac{25}{2}(2)^2-10(2)-\left[-\frac{10}{3}(1)^3+\frac{25}{2}(1)^2-10(1)\right]???
???\frac{10}{3}-\frac52-\frac{80}{3}+\frac{100}{2}-20+\frac{10}{3}-\frac{25}{2}+10???
???\frac{10}{3}-\frac52-\frac{80}{3}+50-20+\frac{10}{3}-\frac{25}{2}+10???
???-\frac{60}{3}-\frac{30}{2}+40???
???-20-15+40???
???5???
This is the area of the region.