Factoring quadratic equations with coefficients
How to factor a trinomial with a leading coefficient
In this lesson we’ll look at methods for factoring quadratic equations with coefficients in front of the ???x^2??? term (that are not ???1??? or ???0???).
Factoring means you’re taking the parts of an expression and rewriting it as parts that are being multiplied together (the factors).
Factoring a quadratic equation means we will write equations of the form ???ax^2+bx+c??? into the form of ???(px+r)(qx+s)???, where ???a,b,c,p,q,s??? are all real numbers and ???a\neq 1,0???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
How to factor trinomials where a≠1
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. :)
Examples of factoring quadratics with coefficients
Example
Factor the quadratic.
???3x^2+5x-2???
Let’s begin by looking at the factors of ???3??? and ???2???. The only factors of ???3??? are ???3??? and ???1???, so we know we'll have
???(3x\ \ \ \ )(x\ \ \ \ )???
The only factors of ???2??? are ???2??? and ???1???, which means we’ll have one of the following.
???(3x \ \ 2)(x \ \ 1)???
???(3x \ \ 1)(x \ \ 2)???
Let’s see what happens if we use the first way.
???(3x \ \ 2)(x \ \ 1)=3x^2 \ \ 3x \ \ 2x \ \ 2???
We need to combine ???3x??? and ???2x??? in such a way that we get ???5x???. But remember that in ???3x^2+5x-2???, the last term ???-2??? is negative, which means one of our signs has to be negative, so the only two possibilities are
???(3x+2)(x-1)=3x^2-3x+2x-2=3x^2-x-2???
???(3x-2)(x+1)=3x^2+3x-2x-2=3x^2+x-2???
But neither of these is correct because we don’t get the ???+5x??? in the middle. Let’s try the second way.
???(3x \ \ 1)(x \ \ 2)=3x^2 \ \ 6x \ \ x \ \ 2???
Can we make ???6x??? and ???x??? into ???5x??? using negative signs? Yes, we can.
???6x-x=5x???
So we finish our factors with a minus sign in front of the ???1??? and a plus sign in front of the ???2???.
???(3x-1)(x+2)???
Let’s try one more.
Factoring means you’re taking the parts of an expression and rewriting it as parts that are being multiplied together (the factors).
Example
Factor the quadratic.
???15x^2+66x-45???
First, we’ll factor out a ???3???, because it’s a common factor between each of the three terms.
???3(5x^2+22x-15)???
Now, let’s factor ???5x^2+22x-15???.
The only factors of ???5??? are ???5??? and ???1???, so we know we’ll have
???(5x \ \ \ \ )(x \ \ \ \ )???
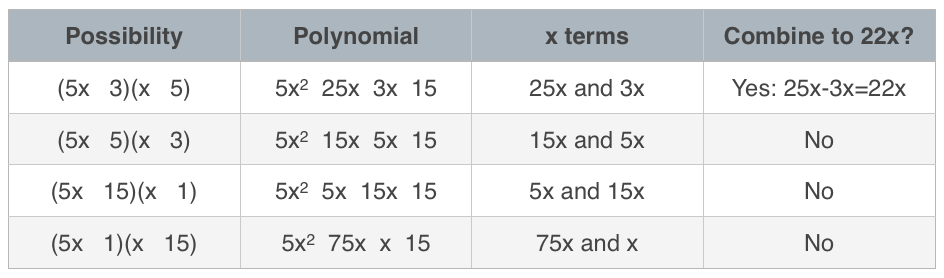
The factor pairs of ???15??? are ???5??? and ???3??? or ???1??? and ???15??? so we know we’ll have one of the following.
From ???5??? and ???3??? we get one of two possibilities:
???(5x \ \ \ 3)(x \ \ \ 5)???
???(5x \ \ \ 5)(x \ \ \ 3)???
From ???1??? and ???15??? we get one of two possibilities:
???(5x \ \ \ 15)(x \ \ \ 1)???
???(5x \ \ \ 1)(x \ \ \ 15)???
Let’s look at the middle terms to see which one can give us ???22x???.
Since there are so many possibilities let’s use a table to help keep them organized.
So we need to use ???(5x \ \ \ 3)(x \ \ \ 5)??? and set it up to get ???25x??? and ???-3x??? when we multiply it out. We get ???(5x-3)(x+5)???. Therefore,
???15x^2+66x-45???
???3(5x^2+22x-15)???
???3(5x-3)(x+5)???