Continuity, and types of discontinuity
Types of discontinuities
You should have some intuition about what it means for a graph to be continuous. Basically, a function is continuous if there are no holes, breaks, jumps, fractures, broken bones, etc. in its graph.
You can also think about it this way: A function is continuous if you can draw the entire thing without picking up your pencil. Let’s take some time to classify the most common types of discontinuity.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Point discontinuity
Point discontinuity exists when there is a hole in the graph at one point. You usually find this kind of discontinuity when your graph is a fraction like this:
???f(x)=\frac{x^2+11x+28}{x+4}???
In this case, the point discontinuity exists at ???x=-4???, where the denominator would equal ???0???. This function is defined and continuous everywhere, except at ???x=-4???. The graph of a point discontinuity is easy to pick out because it looks totally normal everywhere, except for a hole at a single point.
Jump discontinuity
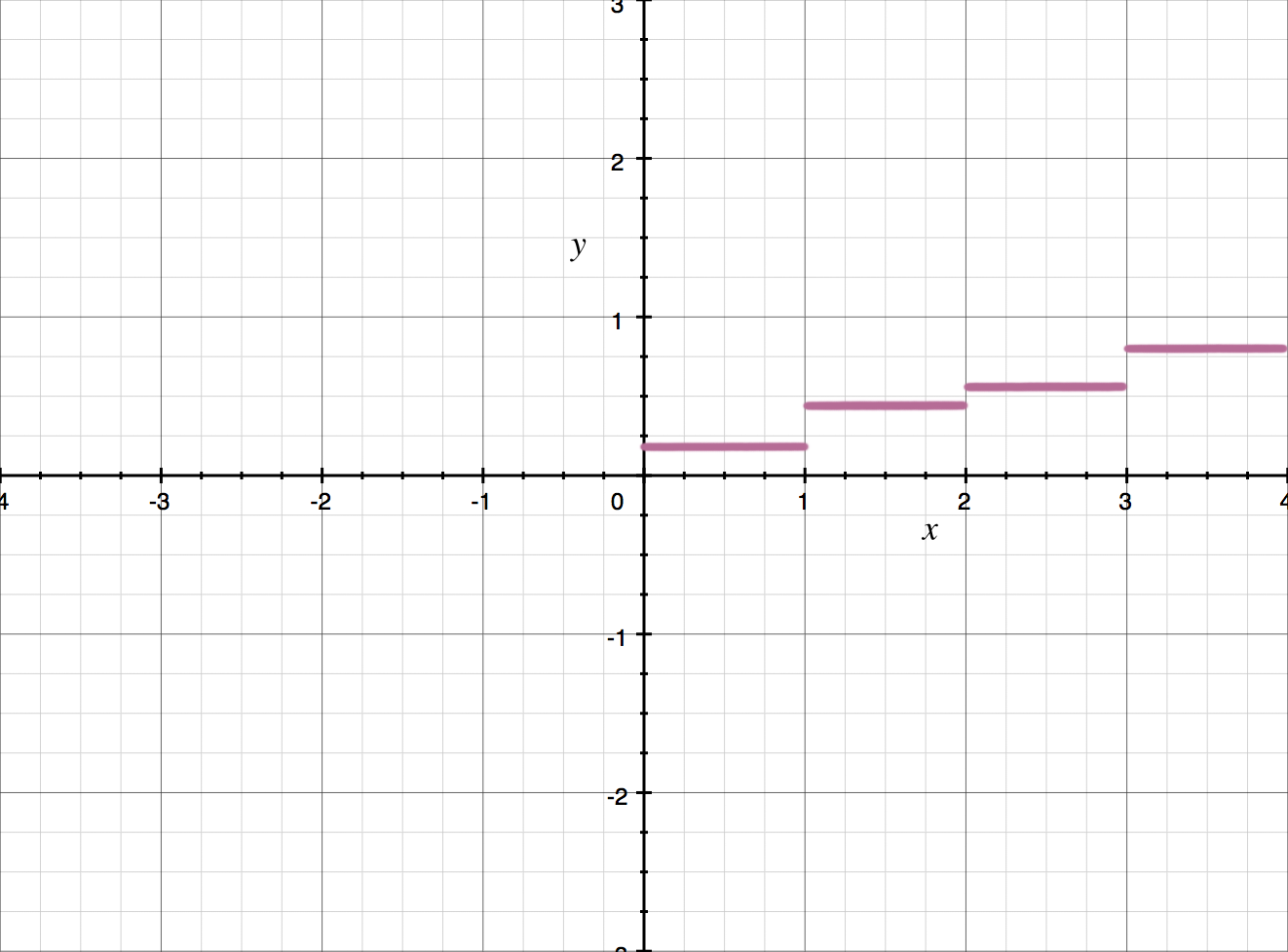
You’ll usually encounter jump discontinuities with piecewise-defined functions, which is a function for which different parts of the domain are defined by different functions. A common example used to illustrate piecewise-defined functions is the cost of postage at the post office.
Below is an example of how the cost of postage might be defined as a function, as well as the graph of the cost function. They tell us that the cost per ounce of any package lighter than ???1??? pound is ???20??? cents per ounce; that the cost of every ounce from ???1??? pound to anything less than ???2??? pounds is ???40??? cents per ounce; etc.
???f(x)=\begin{cases}0.2 & \quad 0<x<1\\0.4 & \quad 1\leq x<2\\0.6 & \quad 2\leq x<3\\0.8 & \quad 3\leq x<4\\1.00 & \quad 4\leq x\end{cases}???
Every break in this graph is a point of jump discontinuity. You can remember this by imagining yourself walking along on top of the first segment of the graph. In order to continue, you’d have to jump up to the second segment.
Infinite (essential) discontinuity
You’ll see this kind of discontinuity called both infinite discontinuity and essential discontinuity. In either case, it means that the function is discontinuous at a vertical asymptote. Vertical asymptotes are only points of discontinuity when the graph exists on both sides of the asymptote.
The graph below shows a vertical asymptote that makes the graph discontinuous, because the function exists on both sides of the vertical asymptote.
On the other hand, the vertical asymptote in this graph is not a point of discontinuity, because it doesn’t break up any part of the graph.