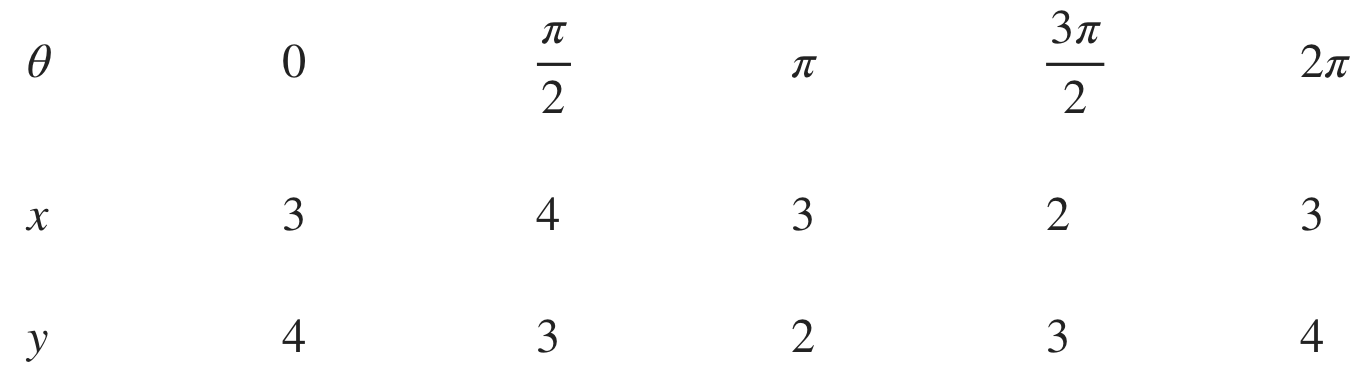Area under one arc or loop of a parametric curve
Finding area under one loop of a parametric curve
Sometimes we need to find the area under just one arc or loop of a parametric curve. In order to do it, we’ll use the area formula
???A=\int^b_a{y(t)}x'(t)\ dt???
where ???[a,b]??? is the interval that contains the loop, and ???x'(t)??? is the derivative of ???x(t)???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
So when we’re given equations for ???x??? and ???y???, we simply plug ???y??? and the derivative of ???x??? into the formula for area.
In order to find the bounds ???[a,b]???, we want to look at the values of ???x??? and ???y??? as the parameter traces out its arc. When the parameter is equal to ???0???, that will correspond to a particular coordinate point ???(x,y)???.
Once the arc arrives back at the same starting point ???(x,y)???, you’ve closed one loop of the curve, and therefore you’ll use the limits of integration that correspond to those parameter values.
To isolate the area of just one loop of the parametric curve, we’ll use bounds on the integral that define the limits of the loop
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Building a table of values to find the bounds that enclose a single loop of the parametric curve
Example
Find the area under the parametric curve over the interval ???0\le\theta\le2\pi???.
???x=3+\sin{\theta}???
???y=3+\cos{\theta}???
The first thing we need to do is find the limits of integration. We’ll set up a chart for ???\theta??? starting at ???0???, and then fill in the corresponding values of ???x??? and ???y???.
Because we started at the point ???(3,4)??? and didn’t return to the same point until the parameter value reached ???2\pi???, the bounds for the integral will be ???[0,2\pi]???.
Before we can plug everything into our area formula, we’ll need to find the derivative of ???x(\theta)???.
???x'(\theta)=\cos{\theta}???
Once the arc arrives back at the same starting point (x,y), you’ve closed one loop of the curve, and therefore you’ll use the limits of integration that correspond to those parameter values.
Plugging everything into the area formula, we get
???A=\int^{2\pi}_0\left(3+\cos{\theta}\right)\left(\cos{\theta}\right)\ d\theta???
???A=\int^{2\pi}_03\cos{\theta}+\cos^2{\theta}\ d\theta???
Before we can integrate, we need to do a substitution for ???\cos^2{\theta}??? using the formula
???\cos^2{\theta}=\frac12(1+\cos{2\theta})???
We’ll make the substitution.
???A=\int^{2\pi}_03\cos{\theta}+\frac12(1+\cos{2\theta})\ d\theta???
???A=\int^{2\pi}_03\cos{\theta}+\frac12+\frac12\cos{2\theta}\ d\theta???
???A=3\sin{\theta}+\frac12\theta+\frac14\sin{2\theta}\Big|^{2\pi}_0???
???A=3\sin{(2\pi)}+\frac12(2\pi)+\frac14\sin{(2(2\pi))}-\left[3\sin{(0)}+\frac12(0)+\frac14\sin{(2(0))}\right]???
???A=3(0)+\pi+\frac14(0)-\left[3(0)+\frac12(0)+\frac14(0)\right]???
???A=\pi???