How to find the area of a trapezoid
What is a trapezoid, and what formula can we use to find its area?
In this lesson we’ll look at how to find the area of a trapezoid.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
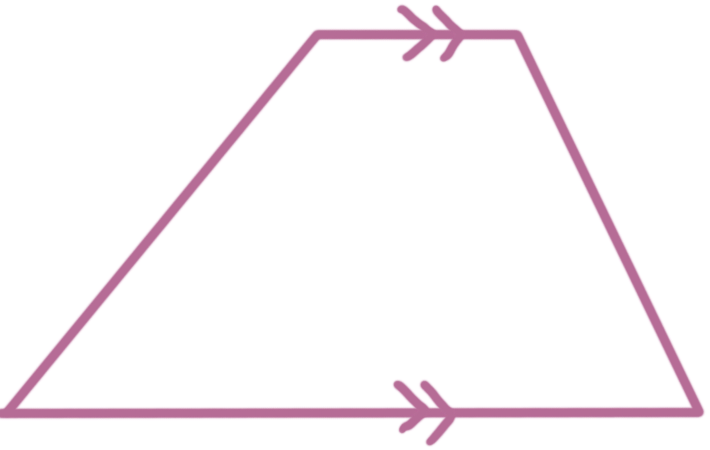
A trapezoid is a quadrilateral with exactly one pair of opposite parallel sides.
Area of a trapezoid
The area of a trapezoid is given by
???A=\frac{1}{2}(b_1+b_2)h???
where ???b_1??? and ???b_2??? are the lengths of the parallel bases, and ???h??? is the height of the trapezoid (which is perpendicular to the parallel bases). Sometimes you’ll need to draw in the height.
The area of a trapezoid is always given in ???\text{units}^2???. Let’s start by working through an example.
How to find the area of trapezoids in different contexts
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Calculating the area of different trapezoids
Example
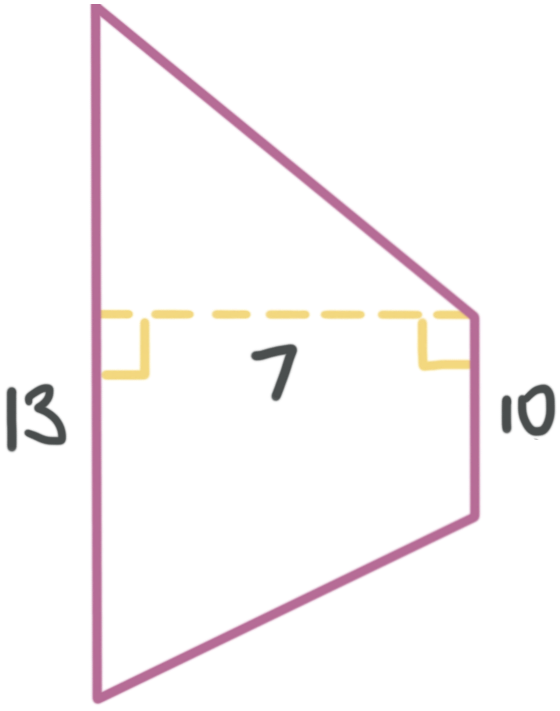
What is the area of the trapezoid?
The bases of a trapezoid are the parallel sides, so this trapezoid has bases of ???13??? units and ???10??? units.
The height of a trapezoid is the length that’s perpendicular to both bases, so this trapezoid has a height of ???7??? units.
???A=\frac{1}{2}(b_1+b_2)h???
???A=\frac{1}{2}(13+10)(7)???
???A=80.5\ \text{units}^2???
Let’s do one more example.
Excerpt
Example
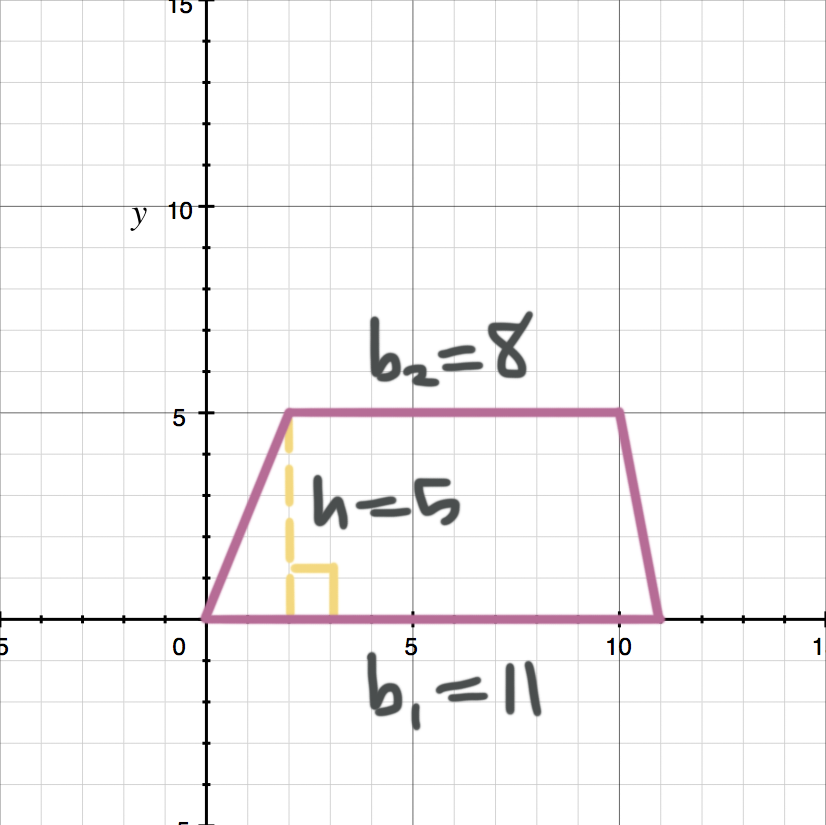
What is the area of the trapezoid in square units?
Use the grid to count the length of the bases and find the height.
Now use the formula for the area of a trapezoid.
???A=\frac{1}{2}(b_1+b_2)h???
???A=\frac{1}{2}(11+8)5???
???A=47.5\ \text{units}^2???