Finding the area of a parallelogram
What is a parallelogram, and how do we find its area?
In this lesson we’ll look at how to find the area of a parallelogram.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
A parallelogram is a quadrilateral with two pairs of opposite parallel sides.
Area of a parallelogram
The area of a parallelogram is found by multiplying the base by the height, so
???A=bh???
The height of a parallelogram needs to be drawn in and is perpendicular to its base.
The units for the area of a parallelogram are always ???\text{units}^2???.
Finding the area of a parallelogram
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Calculating the area of parallelograms
Example
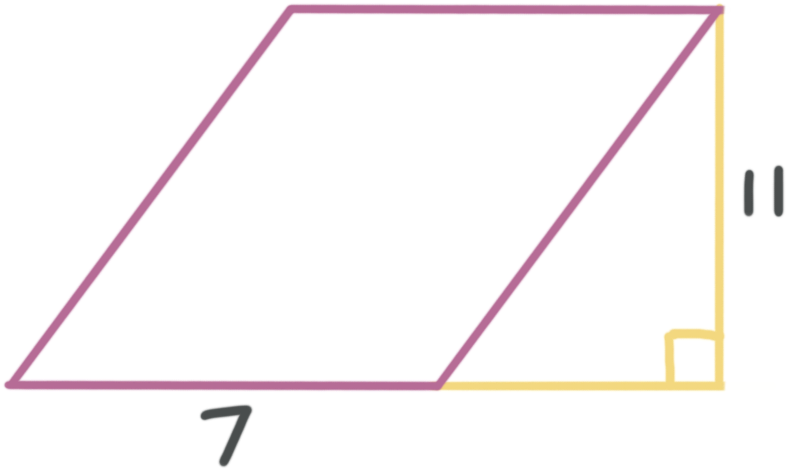
What is the area of the parallelogram?
In this parallelogram, the base has a length of ???7??? units, and a height of ???11??? units, so the area is
???A=7(11)???
???A=77\ \text{units}^2???
Let’s do another example.
The height of a parallelogram needs to be drawn in and is perpendicular to its base.
Example
What is the area of the parallelogram in square units?
Use the grid (the system of horizontal and vertical lines) in the figure to find the dimensions of the parallelogram.
Now we can use the area formula.
???A=bh???
???A=9\ \text{units}\cdot 6\ \text{units}???
???A=54\ \text{units}^2???
Let’s do one with a few more steps.
Example
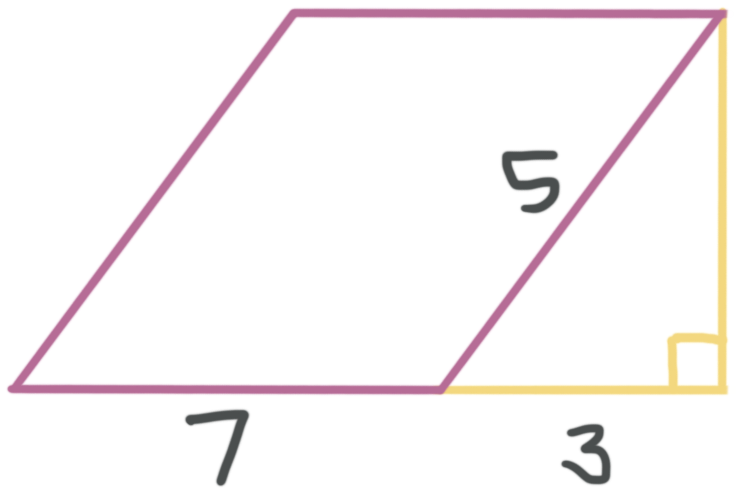
What is the area of the parallelogram in square units?
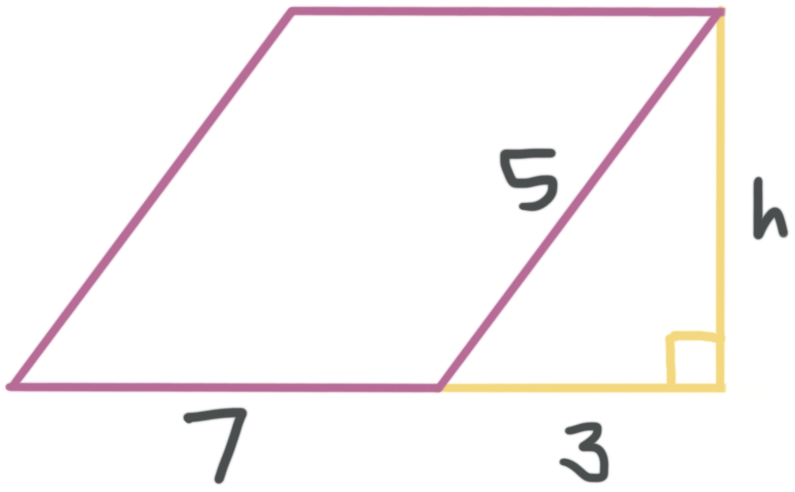
The area of a parallelogram is ???A=bh???. We know the base of the parallelogram is ???7??? units, but we need to find the height. We can see that the yellow lines and the slanted side of the parallelogram form a right triangle, so we can use the Pythagorean theorem to solve for the height. Let’s call the height ???h???.
Then we can plug everything we have into the Pythagorean theorem to find ???h???.
???{{3}^{2}}+{{h}^{2}}={{5}^{2}}???
???9+{{h}^{2}}=25???
???{{h}^{2}}=16???
???h=\pm \sqrt{16}???
???h=\pm 4???
Height can’t take on a negative value, so ???h=4???. Now we can say that the area of the parallelogram is
???A=7\cdot 4???
???A=28\ \text{units}^2???