Finding volume over Type I and Type II regions
Defining Type I and Type II regions as areas of integration
We already know that we can use double integrals to find the volume below a surface over some region ???R=[a,b]\times[c,d]???.
We can define the region ???R??? as Type I, Type II, or a mix of both. Type I curves are curves that can be defined for ???y??? in terms of ???x??? and lie more or less “above and below” each other.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
On the other hand, Type II curves are curves that can be defined for ???x??? in terms of ???y??? and lie more or less “left and right” of each other.
Type I regions can be broken up into vertical slices, and Type II regions can be broken up into horizontal slices.
Sometimes a region can be considered both Type I and Type II, in which case you can choose to evaluate it either way.
Using a double integral to find volume over a Type I or Type II region
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Define the region as Type I or Type II, then find volume over the region
Example
Define the region ???D??? as Type I or Type II, then find volume below the surface over the region ???D???.
???\int\int_Dx^2+6y-20\ dA???
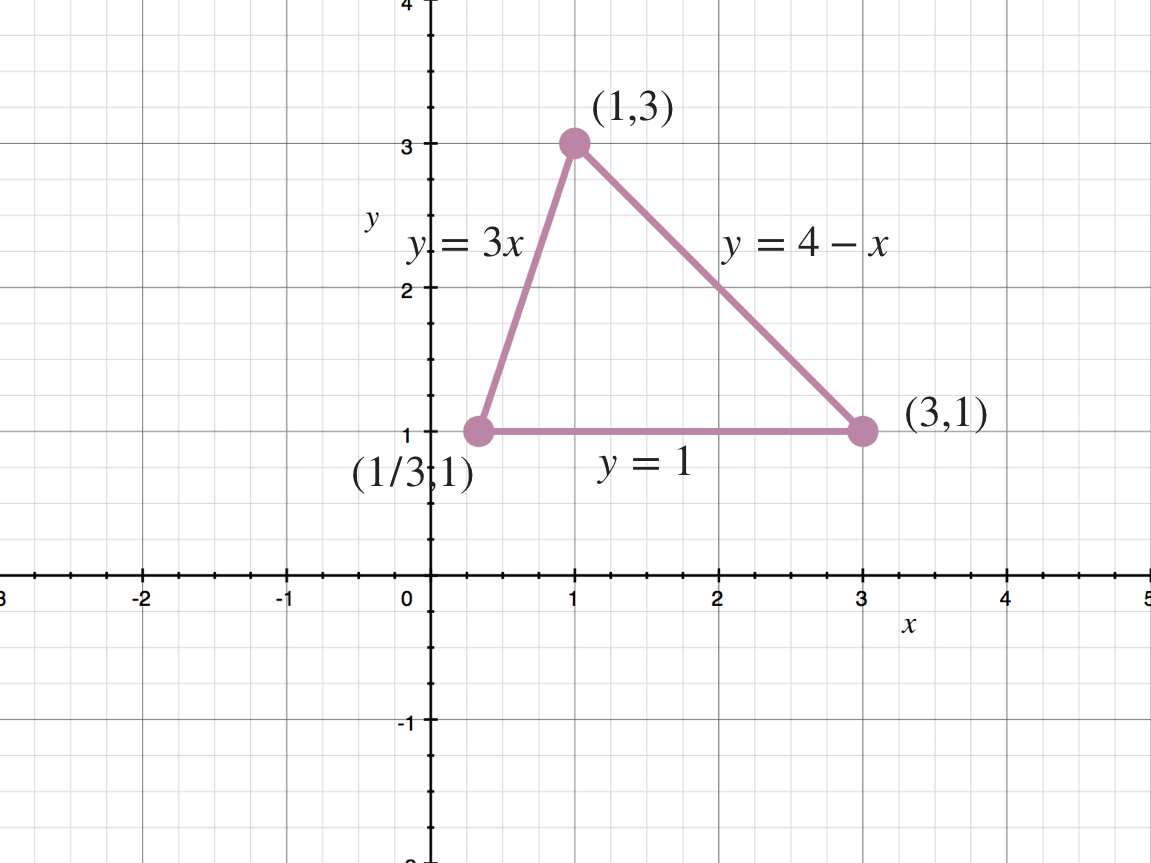
where ???D??? is the triangle bounded by ???y=1???, ???y=3x???, and ???y=4-x???
The first thing we’ll do is sketch the region ???D???. It’ll be easy if we solve for the intersection points of the three lines.
We’ll find the intersection of ???y=1??? and ???y=3x???.
???3x=1???
???x=\frac13???
Pairing ???x=\frac13??? with ???y=1???, the intersection point is ???\left(\frac13, 1\right)???.
We’ll find the intersection of ???y=1??? and ???y=4-x???.
???4-x=1???
???-x=-3???
???x=3???
Pairing ???x=3??? with ???y=1???, the intersection point is ???(3,1)???.
We’ll find the intersection of ???y=3x??? and ???y=4-x???.
???3x=4-x???
???4x=4???
???x=1???
Plugging ???x=1??? into ???y=3x??? to see that ???y=3???, the intersection point is ???(1,3)???.
If we plot these points and sketch the lines that connect them, we see the triangular region ???D???.
Now we need to decide if ???D??? is a Type I or Type II region. Since we can get uniform slices either way (vertical slices if we treat it as a Type I region, or horizontal slices if we treat it as a Type II region), we can choose which type we want to use, and we’ll get the same answer with both methods. We’ll solve it as a Type II region, which means we’ll use horizontal slices of region ???D???.
To solve as Type II, the equations that define the lines that are the edges of region ???D??? need to be defined for ???x??? in terms of ???y???. If we solve each of them for ???x??? we get
???y=3x???
???x=\frac13y???
and
???y=4-x???
???x=4-y???
For a Type II region, we’ll integrate first with respect to ???x???, then with respect to ???y???. The upper limit of integration for ???x??? is given by ???x=4-y??? (because that line defines the top of each of our horizontal slices), and the lower limit of integration for ???x??? is given by ???x=(1/3)y??? (because that line defines the bottom of each of our horizontal slices). For the region ???D???, ???y??? is defined between ???y=1??? and ???y=3??? (???y=3??? comes from the intersection point ???(1,3)???). So the original integral becomes
???\int\int_Dx^{2}+6y-20\ dA???
???\int^3_1\int^{4-y}_{\frac{y}{3}}x^{2}+6y-20\ dx\ dy???
Type I regions can be broken up into vertical slices, and Type II regions can be broken up into horizontal slices.
Evaluating from the inside out and therefore integrating with respect to ???x??? first, we get
???\int^3_1\frac13x^3+6xy-20x\Big|^{x=4-y}_{x=\frac{y}{3}}\ dy???
???\int^3_1\frac13(4-y)^3+6(4-y)y-20(4-y)-\left[\frac13\left(\frac{y}{3}\right)^3+6\left(\frac{y}{3}\right)y-20\left(\frac{y}{3}\right)\right]\ dy???
???\int^3_1\frac13(4-y)(4-y)(4-y)+6y(4-y)-80+20y-\left[\frac13\left(\frac{y^3}{27}\right)+6y\left(\frac{y}{3}\right)-\frac{20y}{3}\right]\ dy???
???\int^3_1\frac13\left(16-8y+y^2\right)(4-y)+24y-6y^2-80+20y-\left(\frac{y^3}{81}+\frac{6y^2}{3}-\frac{20y}{3}\right)\ dy???
???\int^3_1\frac13\left(64-16y-32y+8y^2+4y^2-y^3\right)+24y-6y^2-80+20y-\frac{1}{81}y^3-2y^2+\frac{20}{3}y\ dy???
???\int^3_1\frac13\left(64-48y+12y^2-y^3\right)-\frac{1}{81}y^3-8y^2+44y+\frac{20}{3}y-80\ dy???
???\int^3_1\frac{64}{3}-16y+4y^2-\frac13y^3-\frac{1}{81}y^3-8y^2+\frac{132}{3}y+\frac{20}{3}y-80\ dy???
???\int^3_1-\frac13y^3-\frac{1}{81}y^3+4y^2-8y^2-16y+\frac{132}{3}y+\frac{20}{3}y+\frac{64}{3}-80\ dy???
???\int^3_1-\frac{27}{81}y^3-\frac{1}{81}y^3-4y^2-\frac{48}{3}y+\frac{132}{3}y+\frac{20}{3}y+\frac{64}{3}-\frac{240}{3}\ dy???
???\int^3_1-\frac{28}{81}y^3-4y^2+\frac{104}{3}y-\frac{176}{3}\ dy???
Integrating with respect to ???y???, we get
???-\frac{28}{81}\left(\frac14\right)y^4-4\left(\frac13\right)y^3+\frac{104}{3}\left(\frac12\right)y^2-\frac{176}{3}y\bigg|^3_1???
???-\frac{28}{324}y^4-\frac43y^3+\frac{104}{6}y^2-\frac{176}{3}y\bigg|^3_1???
???-\frac{7}{81}y^4-\frac43y^3+\frac{52}{3}y^2-\frac{176}{3}y\bigg|^3_1???
???-\frac{7}{81}(3)^4-\frac43(3)^3+\frac{52}{3}(3)^2-\frac{176}{3}(3)-\left[-\frac{7}{81}(1)^4-\frac43(1)^3+\frac{52}{3}(1)^2-\frac{176}{3}(1)\right]???
???-\frac{7}{81}(81)-\frac43(27)+\frac{52}{3}(9)-\frac{176}{3}(3)+\frac{7}{81}+\frac43-\frac{52}{3}+\frac{176}{3}???
???-\frac71(1)-\frac41(9)+\frac{52}{1}(3)-\frac{176}{1}(1)+\frac{7}{81}+\frac43-\frac{52}{3}+\frac{176}{3}???
???-7-36+156-176+\frac{7}{81}+\frac{128}{3}???
???-63+\frac{7}{81}+\frac{128}{3}???
???-\frac{5,103}{81}+\frac{7}{81}+\frac{3,456}{81}???
???-\frac{1,640}{81}???
We can say that the volume under the curve ???z=x^{2}+6y-20??? over the region ???D??? is
???-\frac{1,640}{81}???
The fact that the volume is negative means that there is more volume enclosed by the curve and the ???xy???-plane that lies below the ???xy???-plane than the amount that lies above the ???xy???-plane.