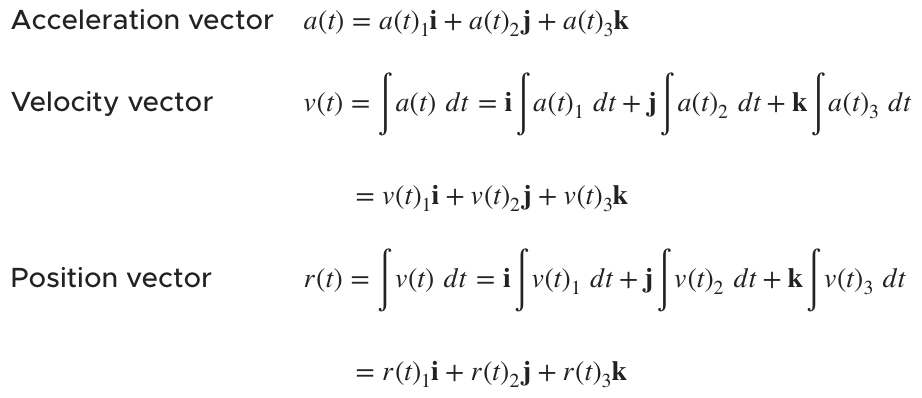How to find velocity and acceleration vectors
Position, velocity, and acceleration vectors
Given a position function ???r(t)??? that models the position of an object over time, velocity ???v(t)??? is the derivative of position, and acceleration ???a(t)??? is the derivative of velocity, which means that acceleration is also the second derivative of position.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Since we know that the derivative of position is velocity, and the derivative of velocity is acceleration, that means that we can also go the other way and say that the integral of acceleration is velocity, and the integral of velocity is position.
Finding velocity and acceleration vectors, given the position vector
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Finding position given acceleration and initial conditions
Example
Find the position function if acceleration is given by ???a(t)=2\bold i+\bold j+3\bold k???, and if ???v(0)=\bold j-\bold k??? and ???r(0)=\bold i+2\bold j-\bold k???.
We’ve been given acceleration, and we need to find position, which means we’ll need to do some integration. We’ll start by integrating acceleration to get to velocity.
???v(t)=\int a(t)\ dt=\bold i\int 2\ dt+\bold j\int 1\ dt+\bold k\int 3\ dt???
???v(t)=2t\bold i+t\bold j+3t\bold k+C???
Without any other information, we wouldn’t be able to solve for the value of ???C???. But since we know that ???v(0)=\bold j-\bold k???, we can plug this initial condition into the velocity function to find a value for ???C???.
???\bold j-\bold k=2(0)\bold i+(0)\bold j+3(0)\bold k+C???
???\bold j-\bold k=C???
Since we know that the derivative of position is velocity, and the derivative of velocity is acceleration, that means that we can also go the other way and say that the integral of acceleration is velocity, and the integral of velocity is position.
Plugging this value for ???C??? back into the velocity function, we get
???v(t)=2t\bold i+t\bold j+3t\bold k+\bold j-\bold k???
???v(t)=2t\bold i+(t+1)\bold j+(3t-1)\bold k???
Now we’ll integrate the velocity function in order to find position.
???r(t)=\int v(t)\ dt=\bold i\int 2t\ dt+\bold j\int t+1\ dt+\bold k\int 3t-1\ dt???
???r(t)=\left(\frac{2}{2}t^2\right)\bold i+\left(\frac{1}{2}t^2+t\right)\bold j+\left(\frac{3}{2}t^2-t\right)\bold k+C_2???
???r(t)=t^2\bold i+\left(\frac{1}{2}t^2+t\right)\bold j+\left(\frac{3}{2}t^2-t\right)\bold k+C_2???
We also have an initial condition for the position function, so we’ll plug that in to find a value for ???C_2???.
???\bold i+2\bold j-\bold k=(0)^2\bold i+\left[\frac{1}{2}(0)^2+0\right]\bold j+\left[\frac{3}{2}(0)^2-0\right]\bold k+C_2???
???\bold i+2\bold j-\bold k=C_2???
Plugging this value for ???C_2??? back into the position function, we get
???r(t)=t^2\bold i+\left(\frac{1}{2}t^2+t\right)\bold j+\left(\frac{3}{2}t^2-t\right)\bold k+\bold i+2\bold j-\bold k???
???r(t)=(t^2+1)\bold i+\left(\frac{1}{2}t^2+t+2\right)\bold j+\left(\frac{3}{2}t^2-t-1\right)\bold k???
This is the position function associated with the given acceleration function and the initial conditions.