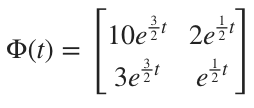Using variation of parameters to solve a system of nonhomogeneous differential equations
Use variation of parameters when undetermined coefficients doesn’t work
If undetermined coefficients isn’t a viable method for solving a nonhomogeneous system of differential equations, we can always use the method of variation of parameters instead.
Just like with undetermined coefficients, we have to start by finding the corresponding complementary solution, which is the general solution of the associated homogeneous equation.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Then we’ll use the complementary solution and the method of variation of parameters to find the particular solution, which will be given by
???\vec{x_p}=\Phi(t)\int \Phi^{-1}(t)F(t)\ dt???
The matrix ???\Phi(t)??? is made of the solution vectors from the complementary solution, and ???\Phi^{-1}(t)??? is its inverse. The vector ???F(t)??? is ???F??? from the nonhomogeneous equation ???\vec{x}'=A\vec{x}+F???.
When we integrate the resulting matrix ???\Phi^{-1}(t)F(t)???, we just integrate each entry in the matrix. And as always, the general solution of the nonhomogeneous system will be the sum of the complementary and particular solutions.
???\vec{x}=\vec{x_c}+\vec{x_p}???
How to solve a nonhomogeneous system of differential equations using the method of variation of parameters
Take the course
Want to learn more about Differential Equations? I have a step-by-step course for that. :)
Step-by-step example of using variation of parameters to solve a system of nonhomogeneous differential equations
Let’s do an example with this variation of parameters method so that we can see these steps in action.
Example
Use the method of variation of parameters to find the general solution of the system.
???x_1'(t)=3x_1-5x_2+e^{\frac{t}{2}}???
???x_2'(t)=\frac34x_1-x_2-e^{\frac{t}{2}}???
Start by writing the nonhomogeneous system in matrix form.
We have to start by finding the complementary solution, which is the general solution to the associated homogeneous equation, which means we need to solve
The coefficient matrix is
and the matrix ???A-\lambda I??? is
Its determinant is
So the characteristic equation is
???\lambda^2-2\lambda+\frac{3}{4}=0???
???\left(\lambda-\frac32\right)\left(\lambda-\frac12\right)=0???
We have to start by finding the complementary solution, which is the general solution to the associated homogeneous equation.
Then for these Eigenvalues, ???\lambda_1=3/2??? and ???\lambda_2=1/2???, we find
Put these two matrices into reduced row-echelon form.
If we turn these back into systems of equations, we get
???k_1-\frac{10}{3}k_2=0???
???k_1=\frac{10}{3}k_2???
and
???k_1-2k_2=0???
???k_1=2k_2???
For the first system, we choose ???(k_1,k_2)=(10,3)???. And from the second system, we choose ???(k_1,k_2)=(2,1)???.
Then the solutions to the system are
Therefore, the complementary solution to the nonhomogeneous system, which is also the general solution to the associated homogeneous system, will be
Now we can turn to finding the particular solution. We’ll use the solution vectors ???\vec{x_1}??? and ???\vec{x_2}??? to form ???\Phi(t)???,
then we’ll find its inverse ???\Phi^{-1}(t)??? by changing ???[\Phi(t) | I]??? into ???[I | \Phi^{-1}(t)]???.
Now with
the particular solution from the method of variation of parameters is given by
Integrate, then simplify the result.
Summing the complementary and particular solutions gives the general solution to the nonhomogeneous system of differential equations.