How to use the triangle side-splitting theorem
What does triangle side-splitting theorem say?
In this lesson we’ll look at the triangle side splitting theorem and how it relates to solving for missing pieces of information in the triangles.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
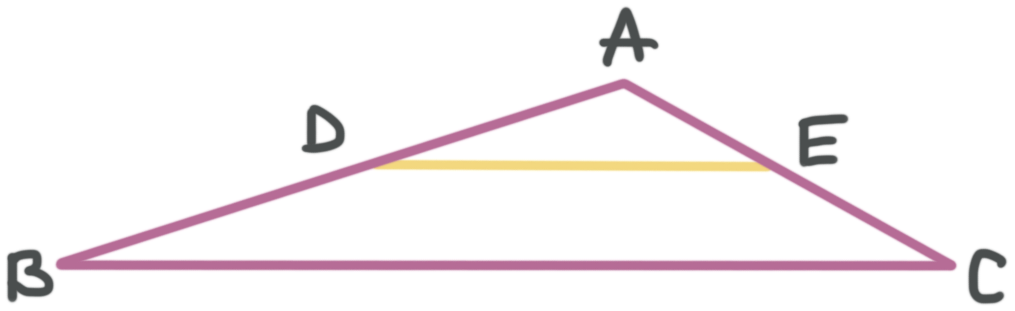
Triangle side-splitting theorem
A triangle can be split by a line segment at any spot in the triangle. As long as the segment touches two sides of the triangle, and is parallel to the side it doesn’t touch, then the segment splits the triangle proportionally.
In the triangle below, the segment ???DE??? is parallel to ???BC???, ???DE\parallel BC???. Because the segment divides the triangle proportionally,
???\frac{AD}{DB}=\frac{AE}{EC}???
How to use triangle side-splitting theorem to solve a triangle
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
How to solve triangle side-splitting theorem problems
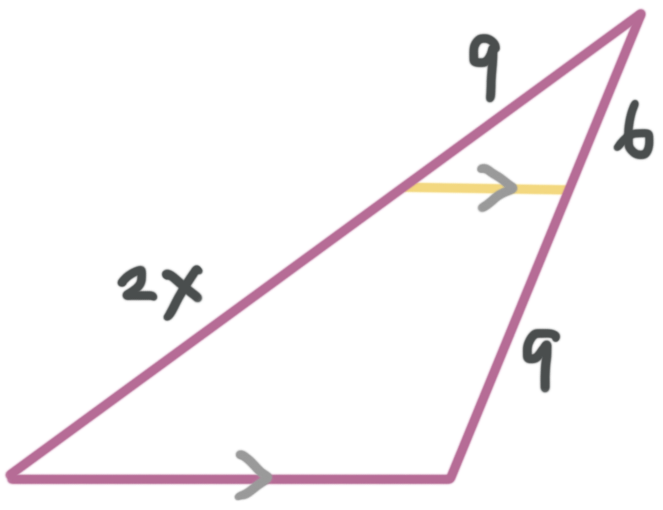
Example
In the figure, the triangle is being split by a segment. Solve for ???x???.
The parallel lines mean that we can use the triangle side-splitting theorem to solve for the variable.
The ratio ???9/2x??? has to be equal to ???6/9???.
???\frac{9}{2x}=\frac{6}{9}???
???9(9)=6(2x)???
???81=12x???
???6.75=x???
Let’s try another one.
A triangle can be split by a line segment at any spot in the triangle. As long as the segment touches two sides of the triangle, and is parallel to the side it doesn’t touch, then the segment splits the triangle proportionally.
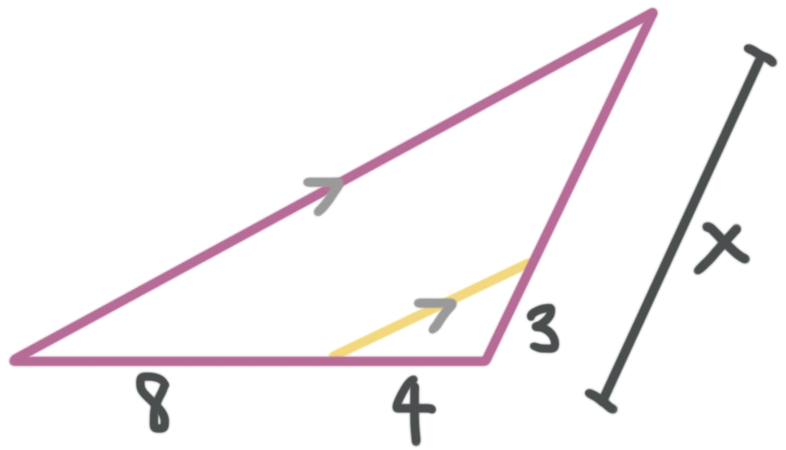
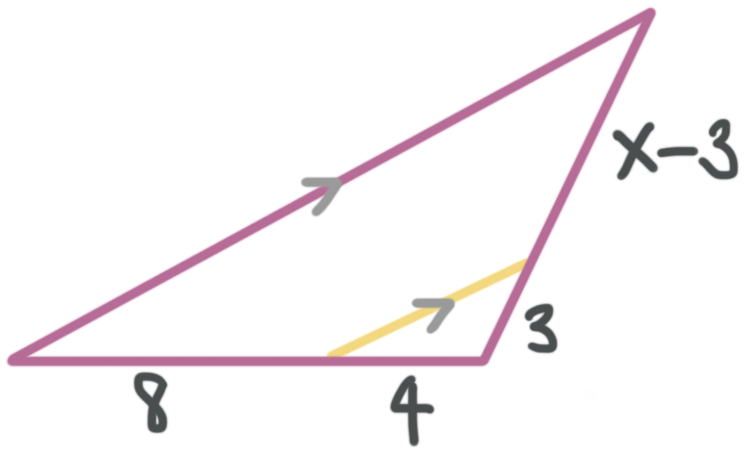
Example
In the figure, the triangle is being split by a segment. Solve for ???x???.
The parallel lines mean that we can use the triangle side-splitting theorem to solve for the variable. We know the length of one side of the larger triangle is ???x???, and that the side length of the smaller triangle along the same side is ???3???. That means the length of that side of the triangle outside of the smaller triangle is ???x-3???.
The ratio ???3/(x-3)??? has to be equal to ???4/8???.
???\frac{3}{x-3}=\frac{4}{8}???
???8(3)=4(x-3)???
???24=4x-12???
???36=4x???
???9=x???