How to translate figures in coordinate space
A translation moves a figure from one position to another
In this lesson we’ll look at how the translation of a figure in a coordinate plane determines where it’s located.
A translation is a transformation that moves a figure in a coordinate plane from one location to another. In this way a translation can be thought of as a slide with no rotating. The slide won’t change the shape or size of the figure, and with no rotation, the orientation won’t change either.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The pre-image and image
A transformation of a shape always starts with the pre-image. The pre-image is usually labeled with capital letters. After the pre-image is translated, the final version of the figure is called the image, which is usually labeled with the same capital letters, plus the prime symbol, ???'???. So if figure ???ABCD??? is translated, its image becomes figure ???A'B'C'D'???.
The image and pre-image are always congruent to each other, because the translation never changes the angles measures or side lengths of the figure.
Translation notation
A translation can be vertical, horizontal, or both. Regardless of the direction, a translation can be written in mathematical notation.
A translation ???3??? units to the left: ???T(x,y)=(x-3,y)???
A translation ???2??? units to the right: ???T(x,y)=(x+2,y)???
A translation ???4??? units down: ???T(x,y)=(x,y-4)???
A translation ???1??? unit up: ???T(x,y)=(x,y+1)???
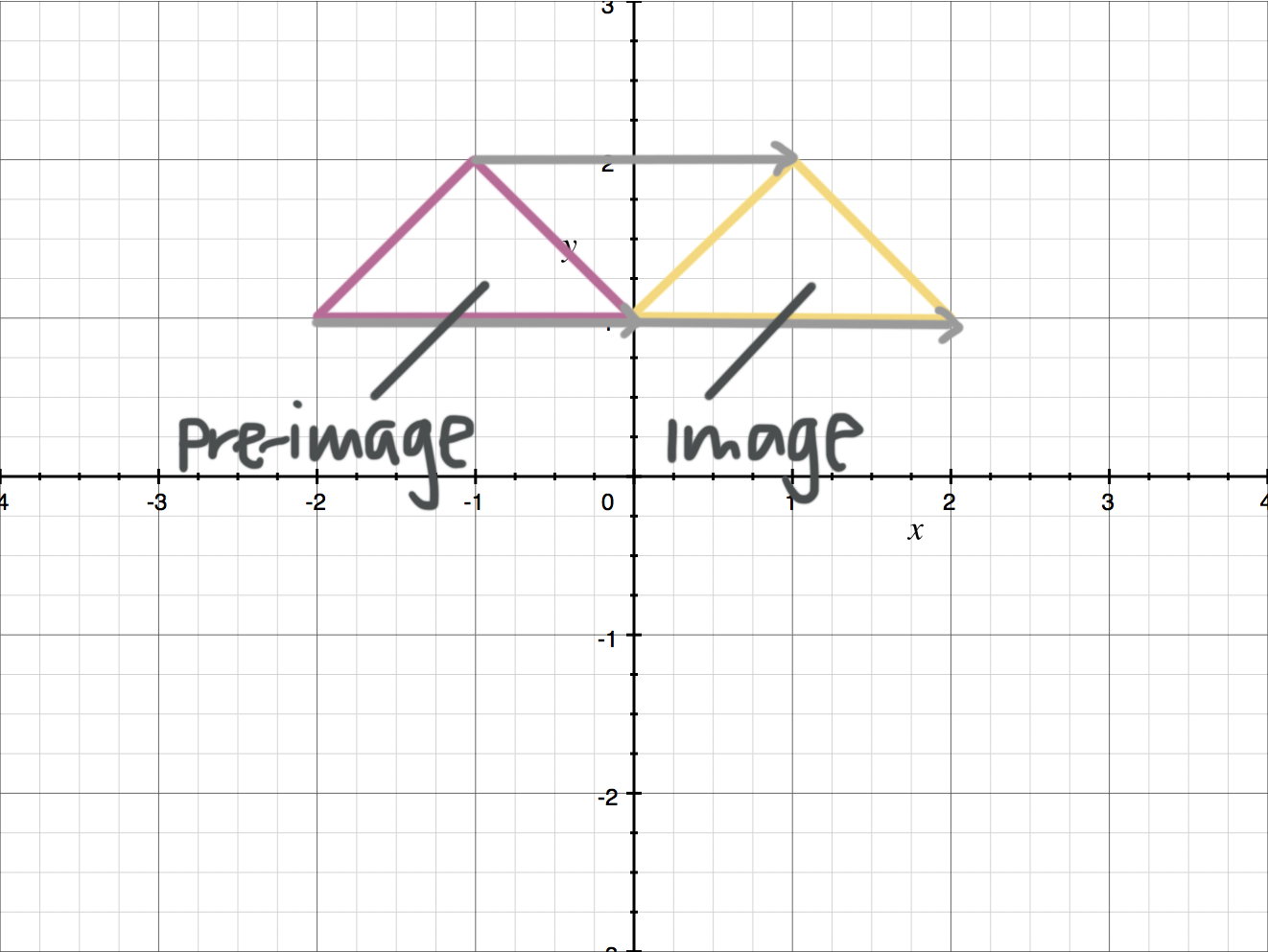
In this triangle translation, the pre-image on the left is translated ???2??? units to the right, ???T(x,y)=(x+2,y)???, in order to get to the image on the right.
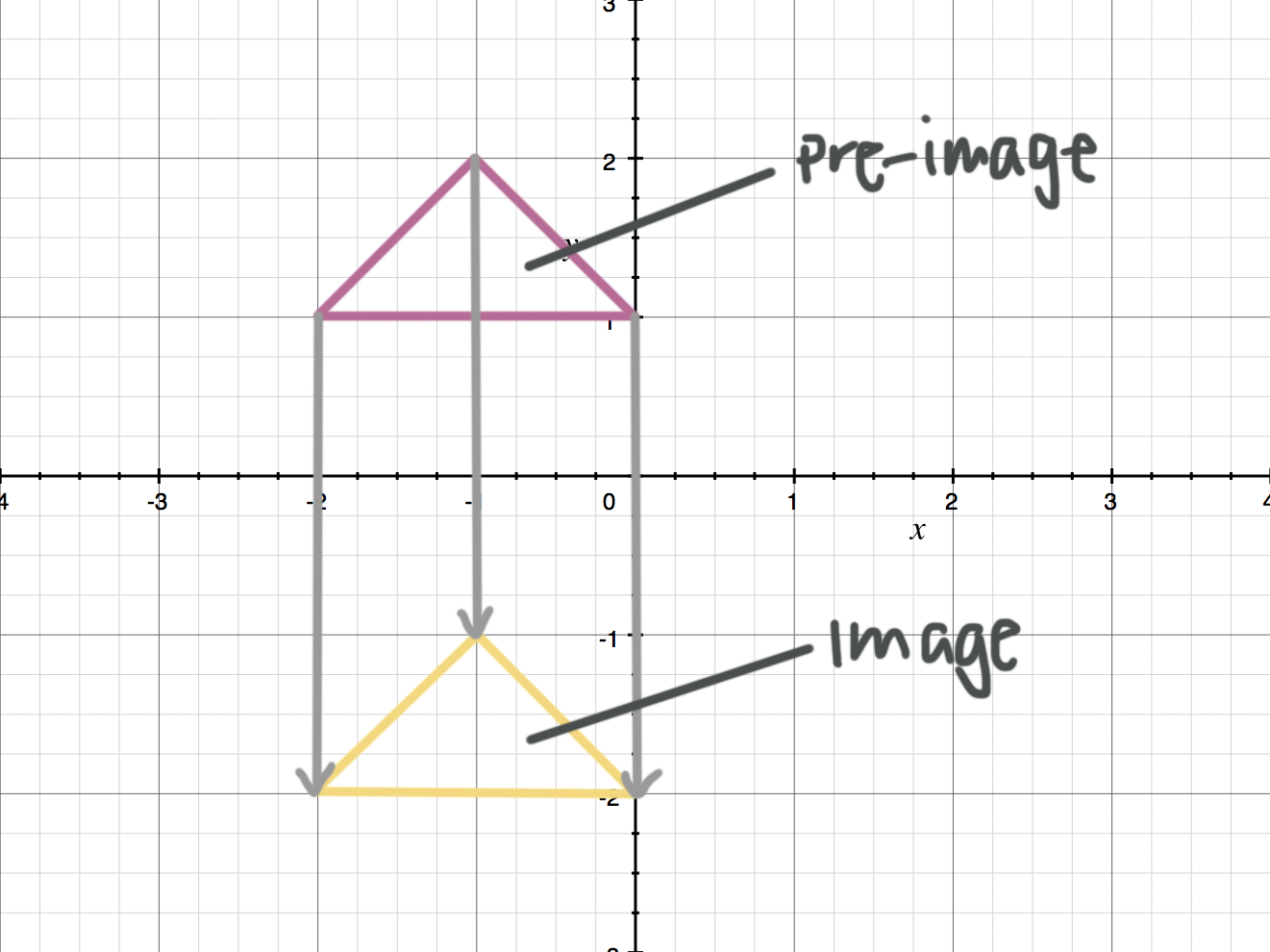
In this triangle translation, the pre-image at the top is translated ???4??? units down, ???T(x,y)=(x,y-4)???, in order to get to the image at the bottom.
Two translations together
We said that we can do a horizontal and vertical translation at the same time. If we want to translate a figure ???2??? units to the right and ???4??? units down, then the translation is
???T(x,y)=(x+2,y-4)???
How to translate figures in coordinate space
Take the course
Want to learn more about Geoemtry? I have a step-by-step course for that. :)
Where is the translated point located?
Example
If rectangle ???ABCD??? undergoes the translation described by ???T(x,y)=(x-2,y+3)???, where will point ???D'??? be located?
The translation is ???T(x,y)=(x-2,y+3)???. The ???x-2??? tells you that in the new set of points, each ???x???-value will now be ???2??? less than it was in the old set of points and each ???y???-value will now be ???3??? more than it was with the old set of points.
In other words, the figure will be located ???2??? units to the left and ???3??? units above the old set of points. The original point ???D??? was ???(-1,-2)???, so the new point ???D'??? will be
???T(-1,-2)=(-1-2,-2+3)=(-3,1)???
So ???D'=(-3,1)???.
Let’s try another translation problem
The slide won’t change the shape or size of the figure, and with no rotation, the orientation won’t change either.
Example
If a translation moves ???A??? to ???A'???, write a rule for the translation if ???A=(-3,7)??? and ???A'=(5,-2)???.
Let’s look at what happens to each coordinate.
The ???x???-value: ???-3\to 5???
This means we added ???8??? because ???-3+8=5???.
For the ???y???-value: ???7\to -2???
This means we subtracted ???9??? because ???7-9=-2???.
Now we can put this all together to write the rule for the translation.
???T(x,y)=(x+8,y-9)???