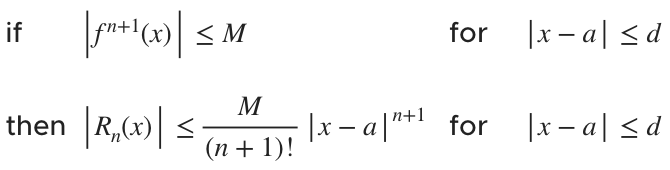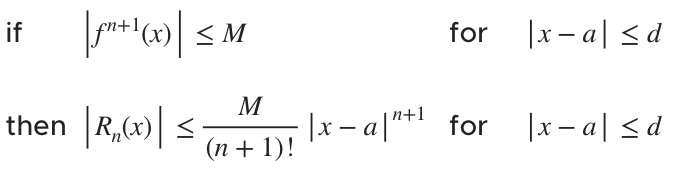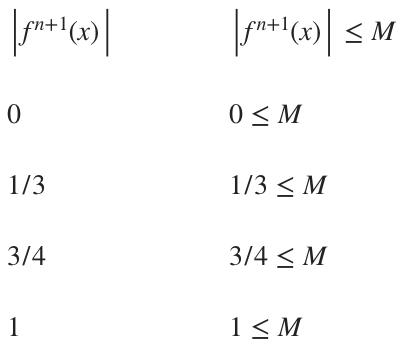Taylor's inequality for the remainder of a series
Taylor’s inequality tells us the maximum remainder of the series
Taylor’s inequality states that, for a function ???f(x)???,
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
This theorem looks elaborate, but it’s nothing more than a tool to find the remainder of a series.
For example, oftentimes we’re asked to find the ???n???th-degree Taylor polynomial that represents a function ???f(x)???. The sum of the terms after the ???n???th term that aren’t included in the Taylor polynomial is the remainder. We can use Taylor’s inequality to find that remainder and say whether or not the ???n???th-degree polynomial is a good approximation of the function’s actual value.
Sometimes we can use Taylor’s inequality to show that the remainder of a power series is ???R_n(x)=0???. If the remainder is ???0???, then we know that the series representation of the function is equal to the exact value of the original function.
If we want to use the theorem to show that the power series representation of the function is equal to the the function itself, then we’ll need to show that both parts of Taylor’s inequality are true and that the remainder is ???0???.
How to use Taylor’s inequality to find the remainder
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Showing that the function’s representation is equal to the original function
Example
Use Taylor’s inequality to show that the the Maclaurin series representation of the function is equal to the original function.
???f(x)=\sin{x}???
Using a table of common Maclaurin series, we know that the power series representation of the Maclaurin series for ???f(x)=\sin{x}??? is
???\sin{x}=\sum^{\infty}_{n=0}\frac{(-1)^nx^{2n+1}}{(2n+1)!}???
In order to show that this equation is true, that the sum of the Maclaurin series is in fact equal to the original function, we’ll need to use Taylor’s inequality to show that the remainder of the power series is ???0???.
Since we’re dealing with a Maclaurin series, ???a=0???, and we can adjust the inequalities from the theorem from
to
or
Next, we’ll need to take the first few derivatives of ???f(x)=\sin{x}??? in order to plug in a value for ???f^{n+1}(x)???.
Since we’ll be taking the absolute value of ???f^{n+1}(x)???, we can say that
???\left|f^{n+1}(x)\right|=\cos{x}???
or
???\left|f^{n+1}(x)\right|=\sin{x}???
We know that ???\cos{x}??? and ???\sin{x}??? only exist between ???-1??? and ???1???, so we could say
???-1\leq\left|f^{n+1}(x)\right|\leq 1???
However, since we’re dealing with absolute value, ???\left|f^{n+1}(x)\right|??? can’t be negative, so
???0\leq\left|f^{n+1}(x)\right|\leq 1???
This inequality tells us that the value of ???|f^{n+1}(x)|??? is somewhere on the interval ???[0,1]???. Let’s pick a few values in the interval and plug them into the first inequality from Taylor’s inequality.
In order to show that this equation is true, that the sum of the Maclaurin series is in fact equal to the original function, we’ll need to use Taylor’s inequality to show that the remainder of the power series is 0.
What we can see is that, if we pick any value ???\left|f^{n+1}(x)\right|<1???, then we won’t be including the whole interval ???[0,1]???. But if we pick ???\left|f^{n+1}(x)\right|=1???, then we know that ???M??? will always be greater than or equal to any value in the interval. Therefore, as a rule, we’ll always pick the right-hand side of the interval. In this case, that’s ???M=1???, which we’ll plug into our already simplified version of Taylor’s inequality.
With Taylor’s inequality simplified after plugging in ???a=0??? and ???M=1???, we’ll use squeeze theorem to evaluate the remainder inequality and try to show that the remainder is ???0???.
???\left|R_n(x)\right|\le{\frac{1}{(n+1)!}}\left|x\right|^{n+1}???
???\lim_{n\to\infty}\left|R_n(x)\right|\le\lim_{n\to\infty}{\frac{1}{(n+1)!}}\left|x\right|^{n+1}???
???\lim_{n\to\infty}\left|R_n(x)\right|\le{\frac{1}{(\infty+1)!}}\left|x\right|^{\infty+1}???
???\lim_{n\to\infty}\left|R_n(x)\right|\le0\cdot\left|x\right|^{\infty}???
???\lim_{n\to\infty}\left|R_n(x)\right|\le0???
By definition, it’s impossible for a remainder to ever be negative, so it must be true that
???\lim_{n\to\infty}\left|R_n(x)\right|=0???
Since the remainder is ???0???, we know that the power series representation of the Maclaurin series of the function is exactly equal to the original function ???f(x)=\sin{x}???.