How to find all four second-order partial derivatives
There are four second-order partial derivatives for every multivariable function
We already learned in single-variable calculus how to find second derivatives; we just took the derivative of the derivative.
Remember how we even used the second derivative to help us with inflection points and concavity when we were learning optimization and sketching graphs?
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Here’s an example from single variable calculus of what a second derivative looks like:
???f(x)=2x^3???
???f'(x)=6x^2???
???f''(x)=12x???
Well, we can find the second derivative of a multivariable function in the same way. Except, instead of just one function that defines the second derivative (like ???f''(x)=12x??? above), we’ll need four functions that define the second derivative! Our second-order partial derivatives will be:
???f_{xx}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^2f}{\partial x^2}???
The derivative with respect to ???x???, of the first-order partial derivative with respect to ???x???
???f_{yy}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^2f}{\partial y^2}???
The derivative with respect to ???y???, of the first-order partial derivative with respect to ???y???
???f_{xy}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^2f}{\partial y\partial x}???
The derivative with respect to ???y???, of the first-order partial derivative with respect to ???x???
???f_{yx}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^2f}{\partial x\partial y}???
The derivative with respect to ???x???, of the first-order partial derivative with respect to ???y???
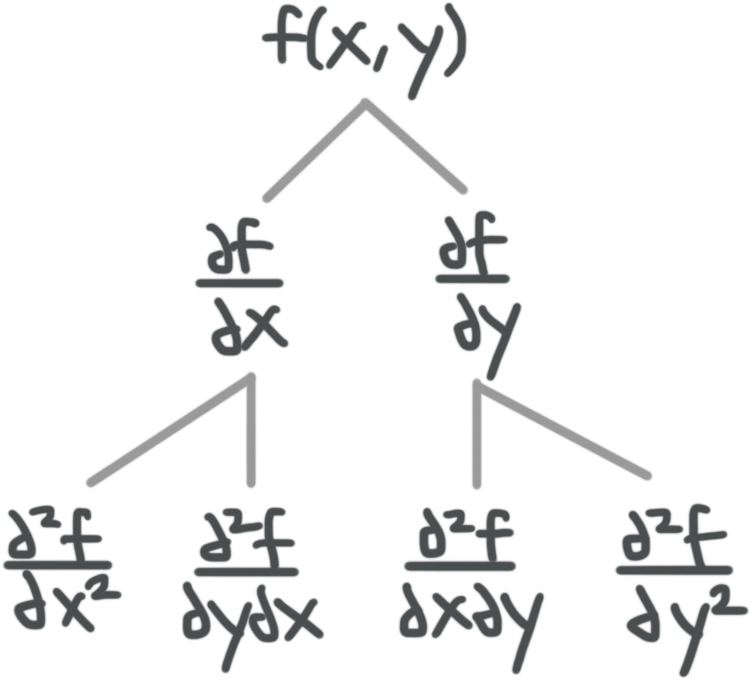
That wording is a little bit complicated. We can think about like the illustration below, where we start with the original function in the first row, take first derivatives in the second row, and then second derivatives in the third row.
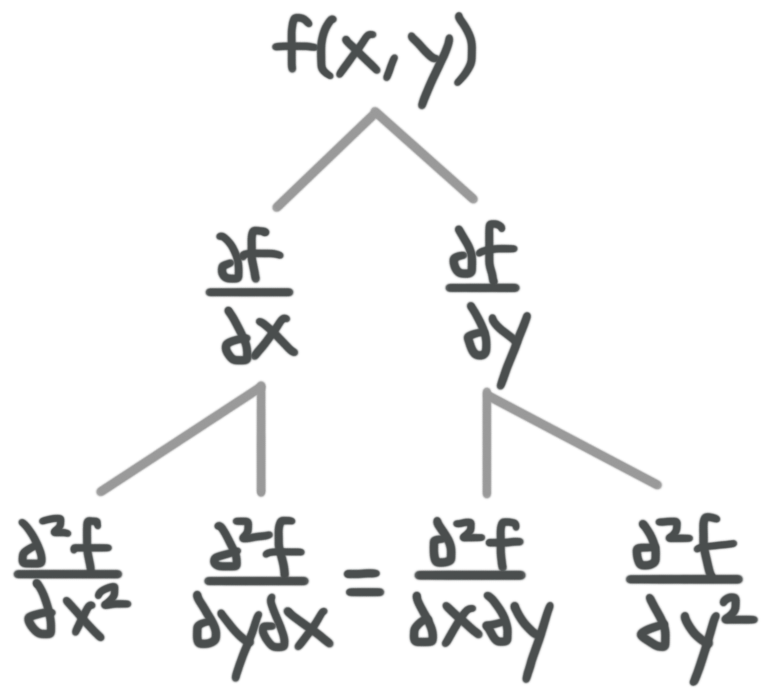
The good news is that, even though this looks like four second-order partial derivatives, it’s actually only three. That’s because the two second-order partial derivatives in the middle of the third row will always come out to be the same.
Whether you start with the first-order partial derivative with respect to ???x???, and then take the partial derivative of that with respect to ???y???; or if you start with the first-order partial derivative with respect to ???y???, and then take the partial derivative of that with respect to ???x???; you’ll get the same answer in both cases. Which means our tree actually looks like this:
How to calculate all four second-order partial derivatives for a multivariable function
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Finding second-order partial derivatives
Example
Find the second-order partial derivatives of the multivariable function.
???f(x,y)=2x^2y???
We found the first-order partial derivatives of this function in a previous section, and they were
???f_x(x,y)=4xy???
???f_y(x,y)=2x^2???
Excerpt
The four second order partial derivatives are:
???f_{xx}=\frac{\partial}{\partial x}(4xy)=4y???
???f_{xy}=\frac{\partial}{\partial x}\left(2x^2\right)=4x???
???f_{yx}=\frac{\partial}{\partial y}(4xy)=4x???
???f_{yy}=\frac{\partial}{\partial y}\left(2x^2\right)=0???
Notice that the mixed second-order partial derivative is the same, regardless of whether you take the partial derivative first with respect to ???x??? and then ???y???, or vice versa.