How to rotate figures in coordinate space around a given rotation point
What is a rotation, and what is the point of rotation?
In this lesson we’ll look at how the rotation of a figure in a coordinate plane determines where it’s located.
A rotation is a type of transformation that moves a figure around a central rotation point, called the point of rotation. The point of rotation can be inside or outside of the figure.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The pre-image and image
A transformation of a shape always starts with the pre-image. The pre-image is usually labeled with capital letters. After the pre-image is rotated, the final version of the figure is called the image, which is usually labeled with the same capital letters, plus the prime symbol, ???'???. So if figure ???ABCD??? is rotated, its image becomes figure ???A'B'C'D'???.
The image and pre-image are always congruent to each other, because the rotation never changes the angles measures or side lengths of the figure.
Rotating figures
To rotate an object you need three things:
a direction (clockwise or counter-clockwise),
an angle (how many degrees you’re rotating), and
the point of rotation
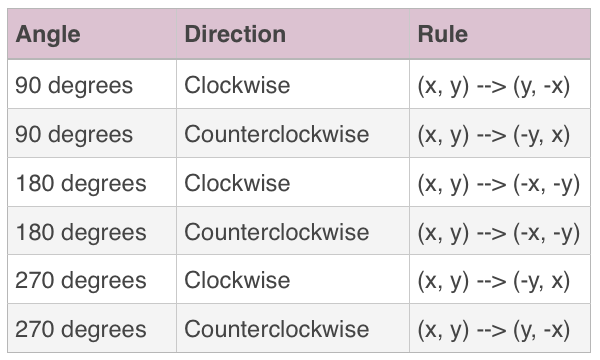
There are some common rotations about the origin ???(0,0)??? that we can use rules for:
If the problem does not give you a direction, then a positive degree measure means a counter-clockwise rotation and a negative degree measure means a clockwise rotation.
How to rotate clockwise and counterclockwise in the coordinate plane
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Writing rules that describe the rotation of the figure
Example
Write a rule to describe the rotation shown in the graph.
You can visually see that the triangle has been rotated ???180^\circ??? about the origin, but you could also look at the rules to see if this follows any of them. Let’s compare the points on the pre-image to the points on the image.
The points on the pre-image are
???A=(-3,2)???
???B=(-2,0)???
???C=(-3,0)???
The points on the image are
???A'=(3,-2)???
???B'=(2,0)???
???C'=(3,0)???
Now we compare the points
???A=(-3,2)\quad\to\quad A'=(3,-2)???
???B=(-2,0)\quad\to\quad B'=(2,0)???
???C=(-3,0)\quad\to\quad C'=(3,0)???
When you compare the points you can see they are following the function rule for a ???180^\circ??? rotation clockwise around the origin.
So the relationship between the pre-image and the image is
???(x,y)\to (-x,-y)???
Let’s try another example.
If the problem does not give you a direction, then a positive degree measure means a counter-clockwise rotation and a negative degree measure means a clockwise rotation.
Example
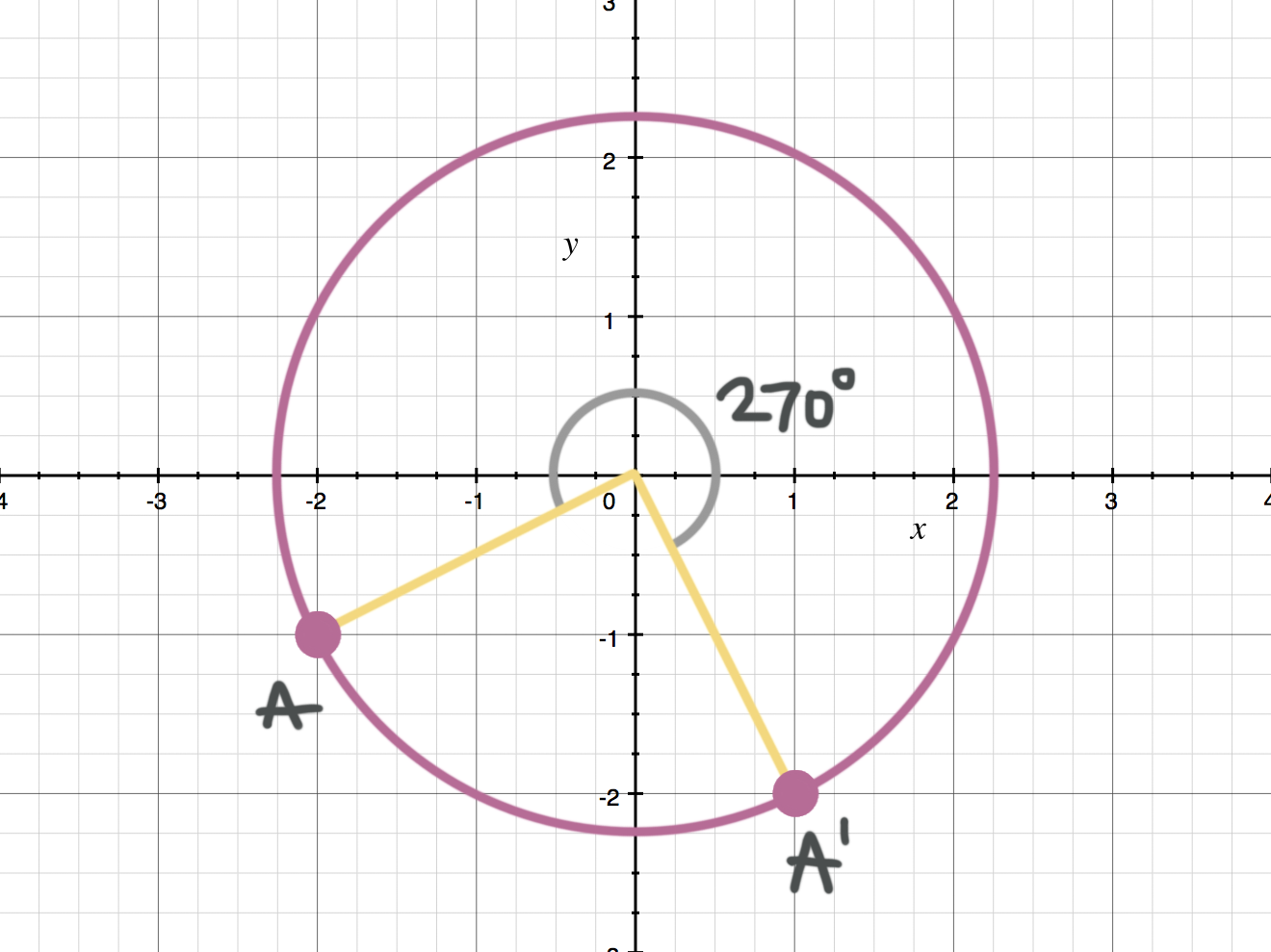
Where will point ???A'??? be located after point ???A??? is rotated ???270^\circ??? clockwise around the origin.
Look up the rule for the rotation of ???270^\circ??? clockwise around the origin.
Point ???A??? is located at ???(-2,-1)???, and we use the rule ???(x,y)\to (-y,x)???. From our original point ???x=-2??? and ???y=-1???. So ???(-2,-1)\to (1,-2)???. The figure shows point ???A??? being rotated ???270^\circ??? clockwise around the origin, ending at ???(1,-2)???.