How to use the Pythagorean theorem
What is the Pythagorean theorem?
In this lesson we’ll look at how to use the Pythagorean theorem to find the length of one side of a right triangle, which is a triangle in which one of the angles is a right angle, that is, a ???90^\circ??? angle) if the lengths of the other two sides are known.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
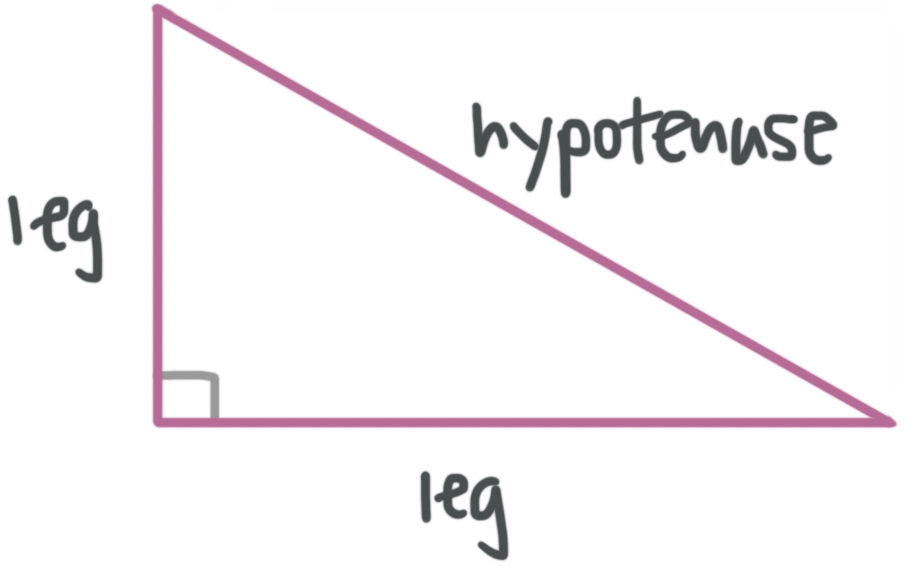
Right triangles
The sides of a right triangle that form the right angle are the legs of the triangle, and the side opposite the right angle is the hypotenuse.
Pythagorean Theorem
The Pythagorean theorem shows how the lengths of the sides of a right triangle are related to one another. It says that the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. We’ll usually see it written as
???{{a}^{2}}+{{b}^{2}}={{c}^{2}}???
You can choose which leg to call leg ???a??? and which leg to call leg ???b???, but the hypotenuse of the triangle is always labeled ???c???.
How to use the Pythagorean theorem with right triangles
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Solving for the length of the third side
Example
Find the length of the hypotenuse.
Since this is a right triangle and we already know the lengths of two of its sides, we can use the Pythagorean theorem to find the length of the third side (in this case the hypotenuse). The Pythagorean theorem is
???{{a}^{2}}+{{b}^{2}}={{c}^{2}}???
Plugging in the lengths we’ve been given (the lengths of the legs), we get
???4^2+12^2=c^2???
???16+144={{c}^{2}}???
???160={{c}^{2}}???
???c=\sqrt{16\cdot 10}???
???c=4\sqrt{10}???
In some problems, the sides of a right triangle are deliberately labeled in a way that’s intended to throw us off, so be careful.
It says that the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.
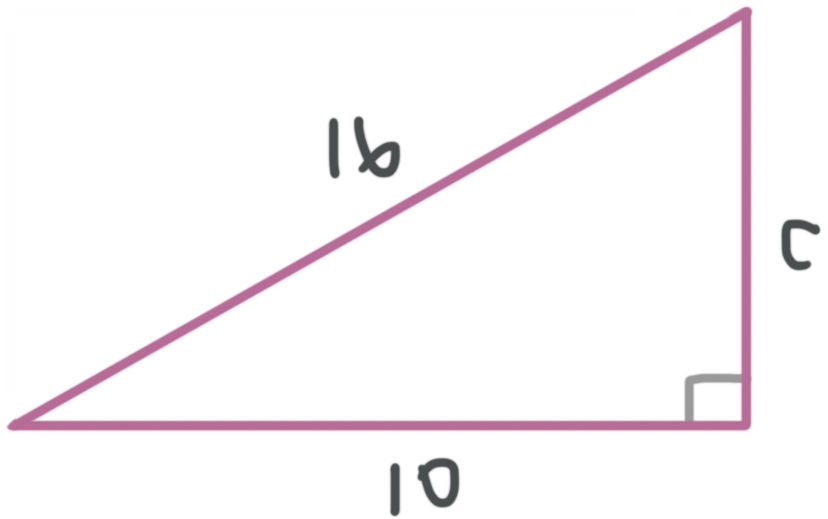
Example
Find the length of side ???c???.
Since this is a right triangle and we already know the lengths of two of its sides, we can use the Pythagorean theorem to find the length of the third side. The only thing we need to notice in this example is that the side labeled ???c??? is not the hypotenuse. Let’s call it side ???a???, since it’s a leg.
The Pythagorean Theorem is
???{{a}^{2}}+{{b}^{2}}={{c}^{2}}???
Plugging in the lengths we’ve been given (in this case the length of the other leg and the length of the hypotenuse), we get
???a^2+10^2=16^2???
???{{a}^{2}}+100=256???
???{{a}^{2}}=156???
???a=\sqrt{4\cdot 39}???
???a=2\sqrt{39}???
Remember that the side we’re calling ???a??? was originally labeled ???c???, so we need to state the answer as
???c=2\sqrt{39}???