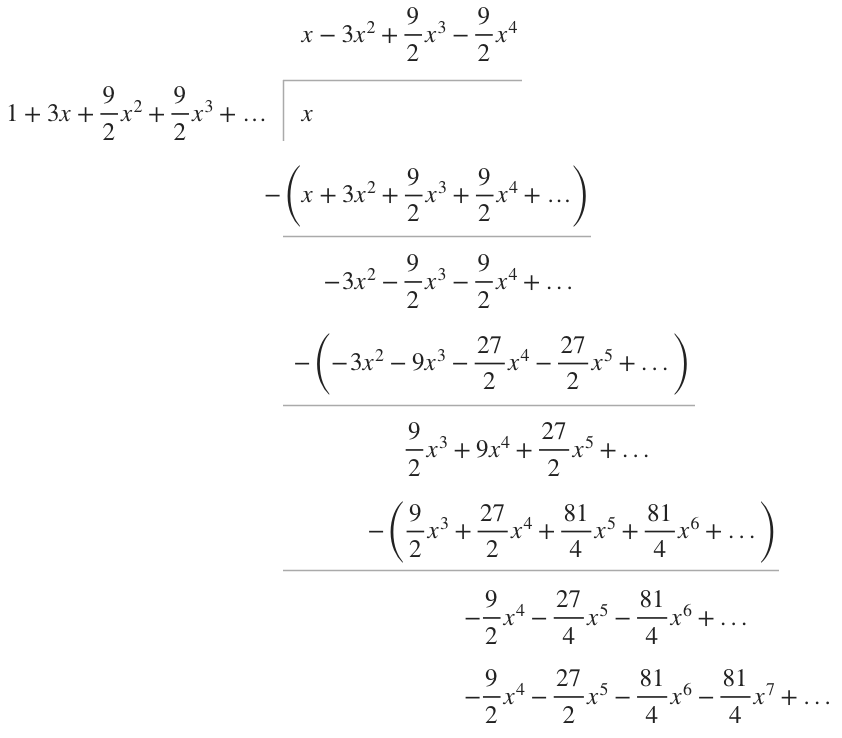Using division to find the power series representation
Replacing a polynomial with its power series expansion
Sometimes we’ll want to use polynomial long division to simplify a fraction, but either the numerator and/or denominator isn’t a polynomial.
In this case, we may be able to replace the non-polynomial with its power series expansion, which will be a polynomial.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
The simplest way to do this for the non-polynomial is to find a similar, known power series expansion and then modify it to match the non-polynomial function.
Once we have polynomial expressions for both the numerator and denominator, we’ll do polynomial long division until we have the number of non-zero terms we’ve been asked for.
How to use division to find a power series expansion
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Turning an equation into a power series by using polynomial long division
Example
Use power series division to find the first three non-zero terms of the Maclaurin series of the given function.
???y=\frac{x}{e^{3x}}???
In order to use long division, we need polynomials in the numerator and denominator of our function. The numerator is already a polynomial, but we need to find a power series expansion for ???e^{3x}??? so that we can change it into a polynomial.
We know that the expanded version of the Maclaurin series for ???e^x??? is
???e^x=\sum^{\infty}_{n=0}\frac{1}{n!}x^n=1+x+\frac12x^2+\frac16x^3+...???
Since we have ???e^{3x}??? instead of ???e^x???, we’ll need to modify the series, letting ???x=3x???, such that the expanded series will be
???e^{3x}=1+3x+\frac12(3x)^2+\frac16(3x)^3+...???
???e^{3x}=1+3x+\frac92x^2+\frac92x^3+...???
Once we have polynomial expressions for both the numerator and denominator, we’ll do polynomial long division until we have the number of non-zero terms we’ve been asked for.
Now that both the numerator and denominator are represented as polynomials, we’ll do the long division.
Remember, we only need to find the first three non-zero terms. We’ll take the first three terms from our quotient and say that the first three non-zero terms are
???y=\frac{x}{e^{3x}}\approx x-3x^2+\frac92x^3???
Text