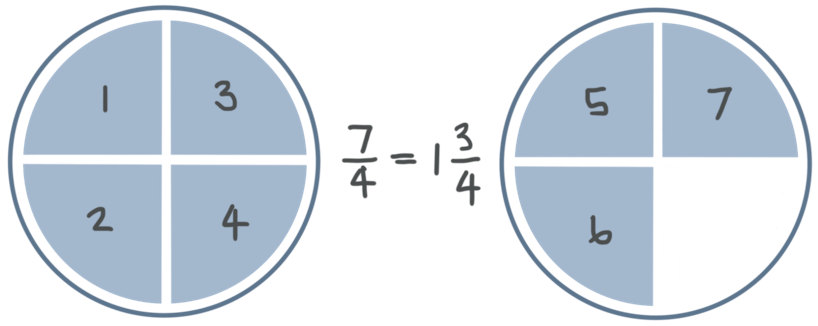Converting between mixed numbers and improper fractions
Converting improper fractions to mixed numbers
In this lesson, we're going to focus on particular kinds of fractions. We'll start out by talking about positive fractions, and then we’ll deal with negative fractions at the end of the lesson.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Up until now, most of the fractions we’ve dealt with are what we call “proper” fractions, where the numerator is less than the denominator. Here are some examples of proper fractions:
Now we’re introducing a new kind of fraction, called an “improper” fraction, where the numerator is greater than or equal to the denominator. In other words, improper fractions are “top-heavy.” Here are some examples of improper fractions:
Even though “improper” sounds like a bad thing, there’s nothing bad about improper fractions. In the same way that a proper fraction represents a positive number less than ???1???, an improper fraction represents a number that’s greater than or equal to ???1???.
For example, ???7/4??? (“seven-fourths”) means seven times ???1/4???, or ???1/4??? seven times. Each of the gray sections below represents ???1/4??? of a circle, and we have seven of them.
As you can see, this is the same thing as saying that we have one circle plus three-fourths of a circle, because we have one full circle on the left and ???3/4??? of a circle on the right.
Now, we just said that
???\frac74=1\frac34???
We know ???7/4??? is an improper fraction. And
???1\frac34???
(“one and three-fourths”) called a mixed number, because it’s a mix of the whole number ???1??? and the fraction ???3/4???. ???1??? is the number of complete circles we have, and ???3/4??? is the portion of a circle that’s left over.
If we summarize what we know so far, we can say that there are three types of fractions:
It’s important to know that we can always convert improper fractions to mixed numbers, and vice versa. For example, you’d write “two and three-sevenths” as
???2\frac37???
Remember,
Converting mixed numbers to improper fractions
If we want to convert a positive mixed number to an improper fraction, we follow these steps:
Multiply the fraction’s denominator by the whole number
Add the result to the fraction’s numerator
Write that result on top of the original denominator
How to work with fractions, improper fractions, and mixed numbers
Take the course
Want to learn more about Pre-Algebra? I have a step-by-step course for that. :)
Convert the mixed number to an improper fraction
Example
Convert the mixed number to an improper fraction.
???2\frac37???
We know that
???2??? is the whole number
???3/7??? is the fraction
???3??? is the fraction’s numerator
???7??? is the fraction’s denominator
We need to multiply the fraction’s denominator (???7???) by the whole number (???2???).
???7\times2=14???
Then we add the fraction’s numerator (???3???) to the result of that multiplication (???14???).
???14+3=17???
This result (???17???) will be the numerator of our improper fraction, and we’ll keep the original denominator (???7???) to get the final answer:
???\frac{17}{7}???
In other words,
???2\frac37=2+\frac37=\frac{7\times2}{7}+\frac37=\frac{7\times2+3}{7}=\frac{14+3}{7}=\frac{17}{7}???
Converting improper fractions to mixed numbers
If we want to convert an improper fraction to a mixed number, we follow these steps:
Divide the numerator of the improper fraction by its denominator.
Write down the whole number part of that result.
Write down any remainder as the numerator in the fraction part, above the original denominator in the fraction part.
If the remainder of the division is ???0???, that just means you can write the result as a whole number, instead of a mixed number.
Example
Convert the improper fraction to a mixed number.
???\frac{19}{6}???
If we look at the positive multiples of ???6???,
???6\cdot1=6???
???6\cdot2=12???
???6\cdot3=18???
???6\cdot4=24???
we can see that ???6??? goes into ???19??? three times, but not four times, since ???6\cdot3=18??? is still less than ???19??? but ???6\cdot4=24??? isn’t.
That means that ???3??? will be the whole number in our mixed number. Since ???6\cdot3=18???, we have to add ???1??? to get from ???18??? to ???19???, which means the remainder is ???1???. Therefore, that remainder (???1???) will be the numerator of the fraction (in our mixed number), and the denominator of the improper fraction (???6???) will be the denominator of the fraction (in our mixed numbers), so the mixed number that’s equivalent to the original improper fraction is
???3\frac16???
In other words,
???\frac{19}{6}=\frac{18+1}{6}=\frac{(6\cdot3)+1}{6}=\frac{6\cdot3}{6}+\frac16=3+\frac16=3\frac16???
Even though “improper” sounds like a bad thing, there’s nothing bad about improper fractions.
Negative fractions
Just as there are positive proper fractions, positive improper fractions, and positive mixed numbers, there are negative proper fractions, negative improper fractions, and negative mixed numbers.
You have to be careful about signs when you express a negative mixed number as the sum of a whole number and a fraction. Both the whole number and the fraction must be negative. It helps to use grouping symbols (such as parentheses or square brackets) in doing this. For example,
???-2\frac37??? means ???-\left(2+\frac37\right)=-2-\frac37???, not ???-2+\frac37???
Going back to our examples, we find that
???-2\frac37=-\left(2+\frac37\right)=-\left(\frac{7\times2}{7}+\frac37\right)=-\left[\frac{(7\times2)+3}{7}\right]=-\frac{17}{7}???
and
???-\frac{19}{6}=-\left(\frac{18+1}{6}\right)=-\left[\frac{(6\cdot3)+1}{6}\right]=-\left(\frac{6\cdot3}{6}+\frac16\right)=-\left(3+\frac16\right)=-3\frac16???