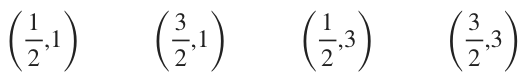Midpoint rule to approximate double integrals
Translating midpoint rule for single integrals into a midpoint rule for double integrals
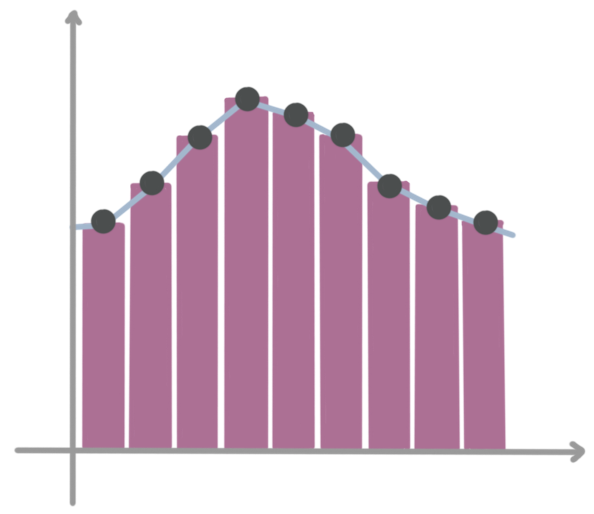
In the past, we used midpoint rule to estimate the area under a single variable function.
We’d draw rectangles under the curve so that the midpoint at the top of each rectangle touched the graph of the function.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Then we’d add the area of each rectangle together to find an approximation of the area under the curve.
When we translate this into three-dimensional space, it means that we use three-dimensional rectangular prisms, instead of two-dimensional rectangles, to approximate the volume under a multivariable function.
And instead of defining an ???x???-interval ???[a,b]??? over which we want to find area, we have to define an ???xy???-interval ???R=[a,b]\times[c,d]??? over which we want to find volume.
The volume under a multivariable function ???f(x,y)??? over the region ???R=[a,b]\times[c,d]??? can be approximated using a double Riemann sum with midpoints.
???\int\int_Rf(x,y)\ dA\approx\sum^m_{i=1}\sum^n_{j=1}f\left(\overline{x_i},\overline{y_j}\right)\Delta{A}???
???m??? is the number of prisms in the ???x???-direction and ???n??? is the number of prisms in the ???y???-direction within the region ???R???. The larger the values of ???m??? and ???n???, the more accurate the approximation will be. Once we know ???R???, ???m??? and ???n???, we can find the midpoint of each prism. ???\Delta {A}??? is the area of the base of one prism, in the same way that ???\Delta x??? was the width of one rectangle when we were using midpoint rule to find area under single variable functions.
How to use the midpoint rule to approximate a double integral
Take the course
Want to learn more about Calculus 3? I have a step-by-step course for that. :)
Midpoint rule when m and n are equal
Example
Use the midpoint rule to approximate the volume under the curve.
???f(x,y)=x+y^2+2???
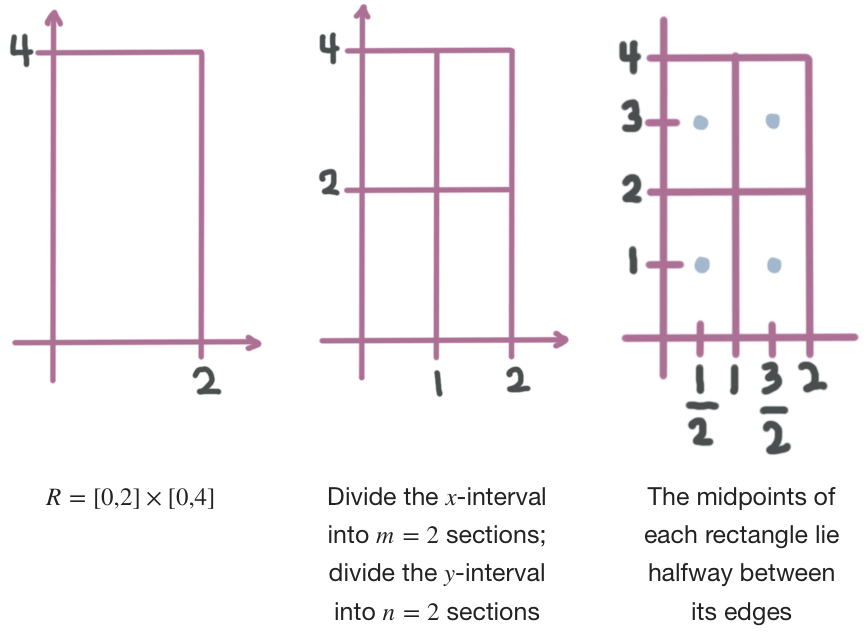
???R=[0,2]\times[0,4]???
???m=n=2???
If we plug the values we’ve been given into the midpoint rule formula, we get
???\int\int_Rf(x,y)\ dA\approx\sum^m_{i=1}\sum^n_{j=1}f\left(\overline{x_i},\overline{y_j}\right)\Delta{A}???
???\int_0^4\int_0^2x+y^2+2\ dx\ dy\approx\sum^2_{i=1}\sum^2_{j=1}f\left(\overline{x_i},\overline{y_j}\right)\Delta{A}???
Notice the double integral on the left side of the equation. We turned it into an iterated integral (where we can integrate with respect to one variable at a time) by attaching the ???x???-interval to the inside integral and the ???y???-interval to the outside integral. Since we put the limits of integration for ???x??? on the inside interval, that means we also have to put ???dx??? on the inside before ???dy???, which comes second since the limits of integration for ???y??? are on the outside integral.
We could evaluate this iterated integral to find exact volume under the curve over the rectangle ???R=[0,2]\times[0,4]???, but we’ve been asked to use midpoint rule to approximate volume, so instead we’ll use the right side of the formula.
We’ll need to define the rectangle ???R???, then divide it into smaller rectangles based on ???m??? and ???n???, and then find the midpoint of each rectangle so that we can plug the midpoints into our function ???f(x,y)=x+y^2+2???, then plug the sum of the results into the approximation formula for ???f\left(\overline{x_i},\overline{y_j}\right)???.
The rectangle ???R=[0,2]\times[0,4]??? means that we want to integrate over the ???x???-interval ???[0,2]??? and over the ???y???-interval ???[0,4]???.
The midpoints of the four smaller rectangles are
When we translate this into three-dimensional space, it means that we use three-dimensional rectangular prisms, instead of two-dimensional rectangles, to approximate the volume under a multivariable function.
We also need to find ???\Delta {A}???, the area of the smaller rectangles. Since the dimensions of the smaller rectangles are ???1\times2???, we can say
???\Delta {A}=(1)(2)???
???\Delta {A}=2???
Plugging each midpoint into the original function ???f(x,y)=x+y^2+2??? and summing the results, we get
???\left[\frac12+(1)^2+2\right]+\left[\frac32+(1)^2+2\right]+\left[\frac12+(3)^2+2\right]+\left[\frac32+(3)^2+2\right]???
We want to plug this sum into the approximation formula for
???\sum^2_{i=1}\sum^2_{j=1}f\left(\overline{x_i},\overline{y_j}\right)???
and also plug in ???\Delta {A}=2???.
???\int_0^4\int_0^2x+y^2+2\ dx\ dy\approx\sum^2_{i=1}\sum^2_{j=1}f\left(\overline{x_i},\overline{y_j}\right)\Delta{A}???
???\int_0^4\int_0^2x+y^2+2\ dx\ dy\approx???
???\left[\left(\frac{1}{2}+(1)^2+2\right)+\left(\frac{3}{2}+(1)^2+2\right)+\left(\frac{1}{2}+(3)^2+2\right)+\left(\frac{3}{2}+(3)^2+2\right)\right](2)???
???\left[\left(\frac12+1+2\right)+\left(\frac32+1+2\right)+\left(\frac12+9+2\right)+\left(\frac32+9+2\right)\right](2)???
???\left[\left(\frac12+3\right)+\left(\frac32+3\right)+\left(\frac12+11\right)+\left(\frac32+11\right)\right](2)???
???\left[\left(\frac12+3\cdot\frac22\right)+\left(\frac32+3\cdot\frac22\right)+\left(\frac12+11\cdot\frac22\right)+\left(\frac32+11\cdot\frac22\right)\right](2)???
???\left[\left(\frac12+\frac62\right)+\left(\frac32+\frac62\right)+\left(\frac12+\frac{22}{2}\right)+\left(\frac32+\frac{22}{2}\right)\right](2)???
???\left[\left(\frac72\right)+\left(\frac92\right)+\left(\frac{23}{2}\right)+\left(\frac{25}{2}\right)\right](2)???
???\frac{64}{2}(2)???
???64???
So we can say that the volume under the function ???f(x,y)=x+y^2+2??? over the region ???R=[0,2]\times[0,4]??? is approximately ???64??? cubic units.