All kinds of measurements for all kinds of quadrilaterals
Let’s start by looking at the properties of all different types of quadrilaterals
A quadrilateral is any closed four-sided figure.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
There are two types of quadrilaterals: concave and convex.
A concave quadrilateral has a part that goes into the shape:
A convex quadrilateral has angles all on the outside corners of the shape:
All convex quadrilaterals have four sides (edges), four corners (vertices) and four interior angles that sum to ???360^\circ???.
Here are some special types of convex quadrilaterals and their properties:
Trapezium
No pairs of parallel sides and no congruent sides
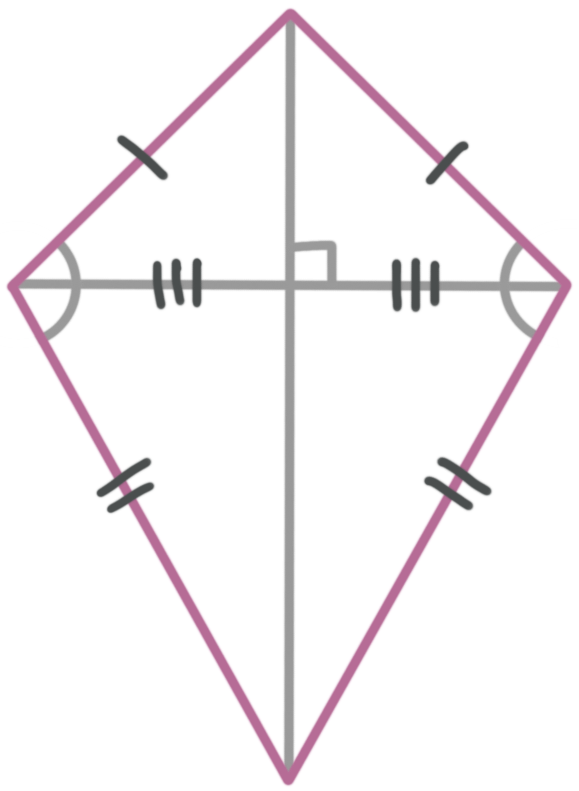
Kite
Has two pairs of adjacent congruent sides
Has a pair of opposite congruent angles
Diagonals cross to form right angles and one of the diagonals bisects the other (cuts it in half)
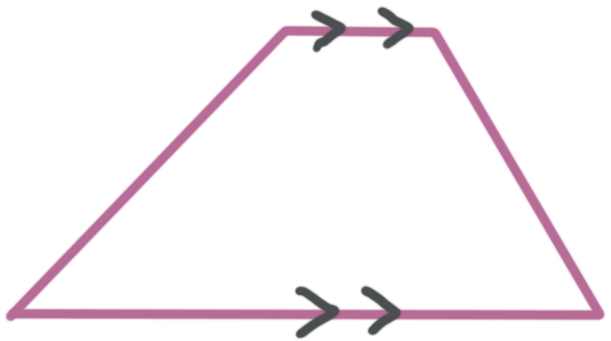
Trapezoid
Has exactly one pair of opposite parallel sides
Isosceles trapezoid
Has exactly one pair of opposite parallel sides
Non-parallel sides have equal lengths
Base angles are congruent
Diagonals are congruent
Parallelogram
Two pairs of opposite parallel sides
Opposite sides are equal lengths
Opposite angles are congruent
???m\angle 1=m\angle 3???
???m\angle 2=m\angle 4???
Consecutive angles are supplementary
???m\angle 1+m\angle 2=180^\circ???
???m\angle 2+m\angle 3=180^\circ???
???m\angle 3+m\angle 4=180^\circ???
???m\angle 4+m\angle 1=180^\circ???
Diagonals bisect each other (cut each other in half)
Rectangle
Two pairs of opposite parallel sides
Opposite sides are equal
All angles are right angles (???90^\circ???)
Diagonals bisect each other (cut each other in half)
Diagonals are congruent
Rhombus/Diamond
Two pairs of opposite parallel sides
All sides are equal lengths
Opposite angles are congruent
Consecutive angles are supplementary
Diagonals are perpendicular bisectors each other (cut each other in half and form right angles)
Square
Two pairs of opposite parallel sides
All angles are right angles
All sides are equal length
Diagonals bisect each other (cut each other in half and form right angles)
How to find measures of the sides, angles, and diagonals of different types of quadrilaterals
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Solving for measures in a parallelogram and a trapezoid
Example
What is the value of ???x??? in the parallelogram?
Angles ???A??? and ???B??? are consecutive angles in a parallelogram (they’re next to each other, not across the figure from one another), so they’re supplementary. Because ???m\angle A=102^\circ??? and ???m\angle B=44^\circ +4x???, we can say
???m\angle A+m\angle B=180{}^\circ???
???102^\circ+44^\circ+4x=180^\circ???
???146^\circ+4x=180^\circ???
???4x=34^\circ???
???x=8.5^\circ???
Let’s look at one more example.
There are two types of quadrilaterals: concave and convex.
A concave quadrilateral has a part that goes into the shape, while
A convex quadrilateral has angles all on the outside corners of the shape.
Example
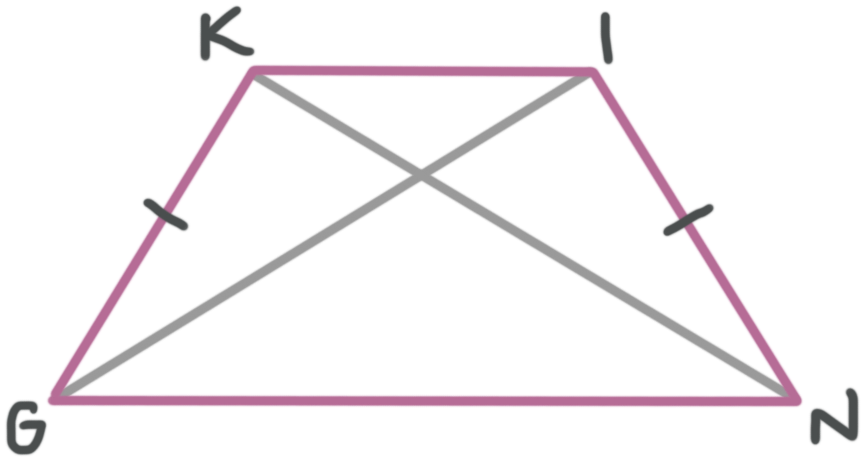
The figure below is a trapezoid. What is the measure of ???KN??? if ???KN=5x+2??? and ???IG=4x+20????
The side lengths of ???KG??? and ???IN??? are marked as being the same length, which means this is an isosceles trapezoid. The diagonals of an isosceles trapezoid are congruent, which means that ???KN=IG???. Therefore,
???KN=IG???
???5x+2=4x+20???
???5x=4x+18???
???x=18???
Then the measure of ???KN??? must be
???KN=5x+2???
???KN=5(18)+2???
???KN=92???