Finding the measure of a circular arc, based on the central angle
Defining the arc length around a circle
In this lesson we’ll look at arcs of circles and how to find their measure.
Arcs
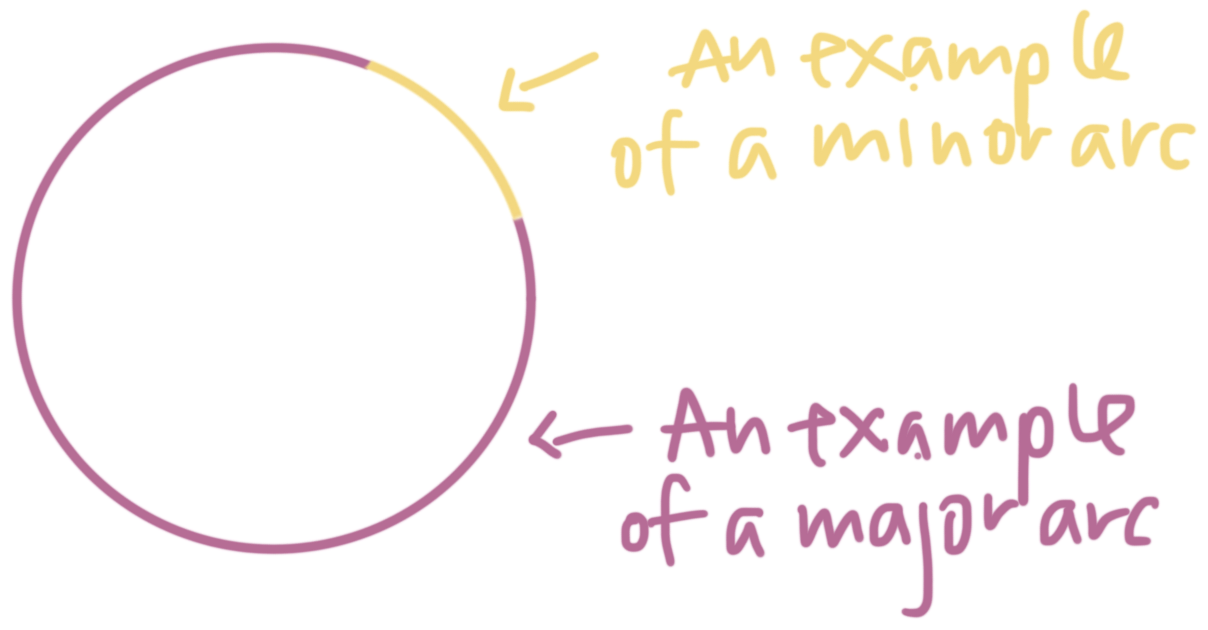
An arc is part of the circumference of a circle. There are three types of arcs.
Minor arcs are less than ???180^\circ???.
Major arcs are more than ???180^\circ???.
Semi-circle arcs are exactly ???180^\circ???.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Measures of arcs and central angles
The central angle of an arc is the angle that connects both ends of the arc and has a vertex at the center of the circle. The central angle and the arc have the same measure. Here the central angle for the minor arc measures ???45^\circ???, so the minor arc is ???45^\circ???.
The central angle for the major arc is ???315^\circ???, so the measure of the major arc is ???315{}^\circ???. The sum of the central angles of a circle always add to ???360{}^\circ???.
Naming arcs and their measures
You can name an arc by the letters that name the beginning and endpoints of the arc on the circle. For example the yellow arc shown below is arc ???AB???. Instead of writing the word arc, we could also use a curved symbol over the letters to indicate the arc, like ???\text{ arc }{AB}???.
The measure of arc ???AB??? is given by the number of degrees in arc ???AB???. Then you add the symbol ???m??? or the word “measure.” In this case we can say the measure of arc ???AB??? is equal to ???45^\circ???. If we used all symbols we could write ???m\text{ arc }{AB}=45^\circ???.
How to find arc length of part of a circle, based on the measure of the central angle
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Finding the difference between arc lengths
Example
If ???\overline{AD}??? is a diameter of the circle (with center at ???C???) in the figure, what is the difference between the measures of ???\overset\frown{DB}??? and arc ???\overset\frown{AE}????
Note: A diameter is any line segment that passes through the center of a circle and has both of its endpoints on the circle. Notice that the diameter is equal to twice the radius, and that the diameter splits a circle into two semicircles. In this problem, ???\overline{AD}??? is a diameter that splits the circle into semicircles ???AD??? and ???DA???.
???\overline{AD}??? is a diameter of the circle, which means that the sum of the measures of arc ???DB??? and arc ???BA??? is ???180^\circ???.
???m\overset\frown{DB}+m\overset\frown{BA}=180^\circ???
???m\overset\frown{DB}+40^\circ=180^\circ???
???m\overset\frown{DB}=140^\circ???
Likewise, the sum of the measures of ???\overset\frown{AE}??? and ???\overset\frown{ED}??? is ???180^\circ???.
???m\overset\frown{AE}+m\overset\frown{ED}=180^\circ???
???m\overset\frown{AE}+130^\circ=180^\circ???
???m\overset\frown{AE}=50^\circ???
The difference between the measures of arcs ???\overset\frown{DB}??? and ???\overset\frown{AE}??? is
???140^\circ -50^\circ =90^\circ???
Let’s look at one more example.
You can name an arc by the letters that name the beginning and endpoints of the arc on the circle.
Example
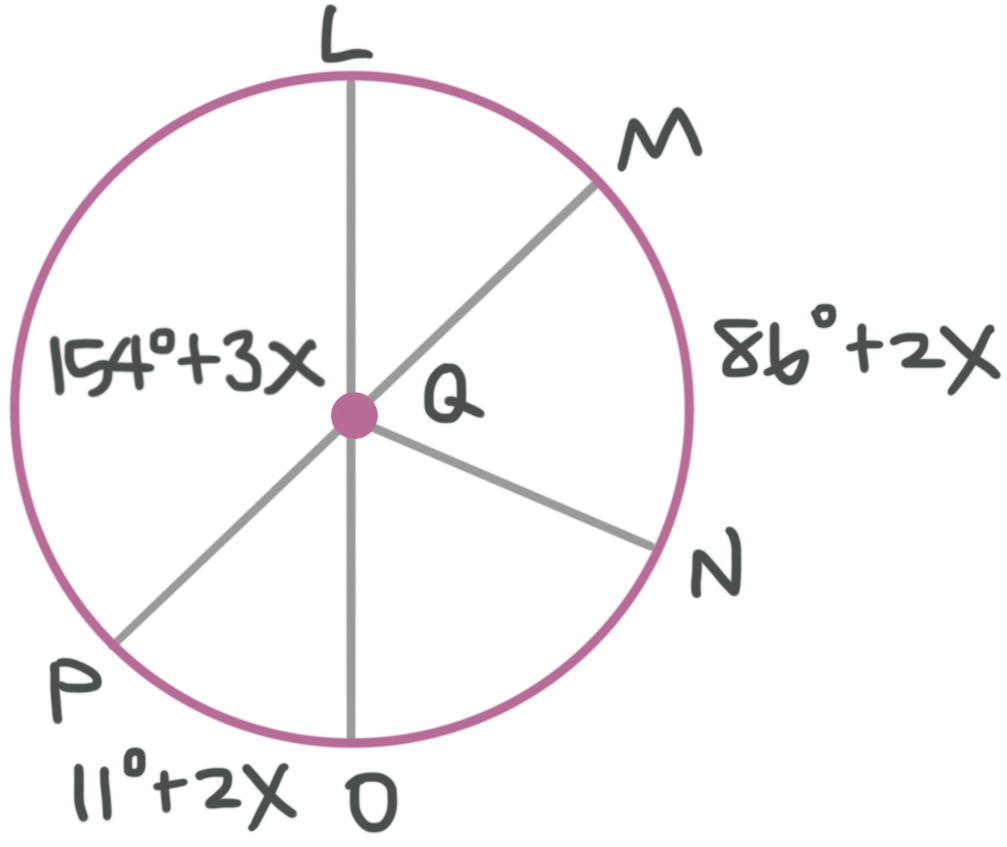
What is the measure of arc ???MN???, given that ???\overline{LO}??? is a diameter of circle ???Q????
We need to solve for ???x??? and then plug it back into the expression for the value of arc ???MN???. We know that ???\overline{LO}??? is a diameter of circle ???Q???, so the sum of the measures of arc ???LP??? and arc ???PO??? is ???180^\circ???.
We can use this information to find the value of ???x???.
???m\text{ arc }{LP}+m\text{ arc }{PO}=180^\circ???
Central angle ???LQP??? has a measure of ???154{}^\circ +3x???, which means that arc ???LP??? also has the same measure. Then we can say
???154^\circ +3x+11^\circ +2x=180^\circ???
???165^\circ +5x=180^\circ???
???5x=15^\circ???
???x=3^\circ???
Now we can find the measure of arc ???MN???.
???m\text{ arc }{MN}=86^\circ +2x???
???m\text{ arc }{MN}=86^\circ +2(3^\circ)???
???m\text{ arc }{MN}=92^\circ???