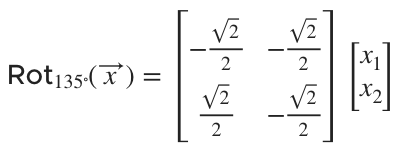Using a linear transformation to represent a rotation
Representing a rotation as a linear transformation
In the previous lesson, we looked at an example of a linear transformation that included a reflection and a stretch. We can apply the same process for other kinds of transformations, like compressions, or for rotations.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
But we can also use a linear transformation to rotate a vector by a certain angle, either in degrees or in radians.
The rotation matrix
Instead of using the appropriate identity matrix like we did for reflecting, stretching, and compressing, we’ll use a matrix specifically for rotations. But the matrix will still always match the dimension of the space in which we’re transforming.
If we’re rotating in ???\mathbb{R}^2???, we’re rotating counterclockwise around the origin through the angle ???\theta???, and the transforming rotation matrix will be
And the transformation to rotate any vector ???\vec{x}??? in ???\mathbb{R}^2??? will be
If we’re rotating in ???\mathbb{R}^3???, the transforming rotation matrix will be different depending on which axis we’re rotating around.
And the transformation to rotate any vector ???\vec{x}??? in ???\mathbb{R}^3??? will be
So if we know the angle by which we’re trying to rotate a vector, we can plug the angle into the rotation matrix, and then multiply the rotation matrix by the vector we want to transform.
We also want to know that rotations follow these properties:
???\text{Rot}_{\theta}(\vec{u}+\vec{v})=\text{Rot}_{\theta}(\vec{u})+\text{Rot}_{\theta}(\vec{v})???
???\text{Rot}_{\theta}(c\vec{u})=c\text{Rot}_{\theta}(\vec{u})???
How to build the transformation matrix for a rotation by a specific angle
Take the course
Want to learn more about Linear Algebra? I have a step-by-step course for that. :)
An example of a rotation in two-dimensional space
Let’s do an example of a rotation in ???\mathbb{R}^2???.
Example
Rotate ???\vec{x}??? by an angle of ???\theta=135^\circ???.
???\vec{x}=(3,2)???
The transformation to rotate any vector ???\vec{x}??? in ???\mathbb{R}^2??? by ???135^\circ??? will be
First, we’ll simplify the rotation matrix. We can get the sine and cosine values at ???\theta=135^\circ??? from the unit circle.
Then the transformation to rotate any vector ???\vec{x}??? in ???\mathbb{R}^2??? by ???135^\circ??? will be rewritten as
So if we know the angle by which we’re trying to rotate a vector, we can plug the angle into the rotation matrix, and then multiply the rotation matrix by the vector we want to transform.
Now we’ll apply this specific rotation matrix to ???\vec{x}=(3,2)???.
If the original vector is ???\vec{x}???, and we call the transformed vector ???\vec{x}_1???, then we can sketch ???\vec{x}??? and ???\vec{x}_1??? and the ???135^\circ??? angle between them.