Finding points of intersection of polar curves
Steps for finding points of intersection of two polar curves
To find the points of intersection of two polar curves,
solve both curves for ???r???,
set the two curves equal to each other
solve for ???\theta???
Using these steps, we might get more intersection points than actually exist, or fewer intersection points than actually exist. To verify that we’ve found all of the intersection points, and only real intersection points, we graph our curves and visually confirm the intersection points.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
We can also convert our polar equations to rectangular equations, solve for the points of intersection of the rectangular curves, and then convert the rectangular points of intersection back into polar coordinates. Even though it’s extra work to convert everything from polar to rectangular, using this method guarantees that we’ll find all of the points of intersection, and only the real points of intersection.
How to find the points of intersection of polar curves
Take the course
Want to learn more about Calculus 2? I have a step-by-step course for that. :)
Two examples of finding intersection points of the polar curves
Example
Find the points of intersection of the polar curves.
???r=\sin{\theta}???
???r=1-\sin{\theta}???
To find the points of intersection of these polar curves, we’ll set them equal to each other and solve for ???\theta???.
???\sin{\theta}=1-\sin{\theta}???
???2\sin{\theta}=1???
???\sin{\theta}=\frac12???
???\theta=\frac{\pi}{6},\ \frac{5\pi}{6}???
To find the values of ???r??? that are associated with these values of ???\theta???, we’ll plug the ???\theta??? values back into either of the original polar curves; we’ll choose ???r=\sin{\theta}???.
For ???\theta=\frac{\pi}{6}???:
???r=\sin{\frac{\pi}{6}}???
???r=\frac12???
For ???\theta=\frac{5\pi}{6}???:
???r=\sin{\frac{5\pi}{6}}???
???r=\frac12???
Putting these values together, the points of intersection are
???\left(\frac12,\frac{\pi}{6}\right)??? and ???\left(\frac12,\frac{5\pi}{6}\right)???
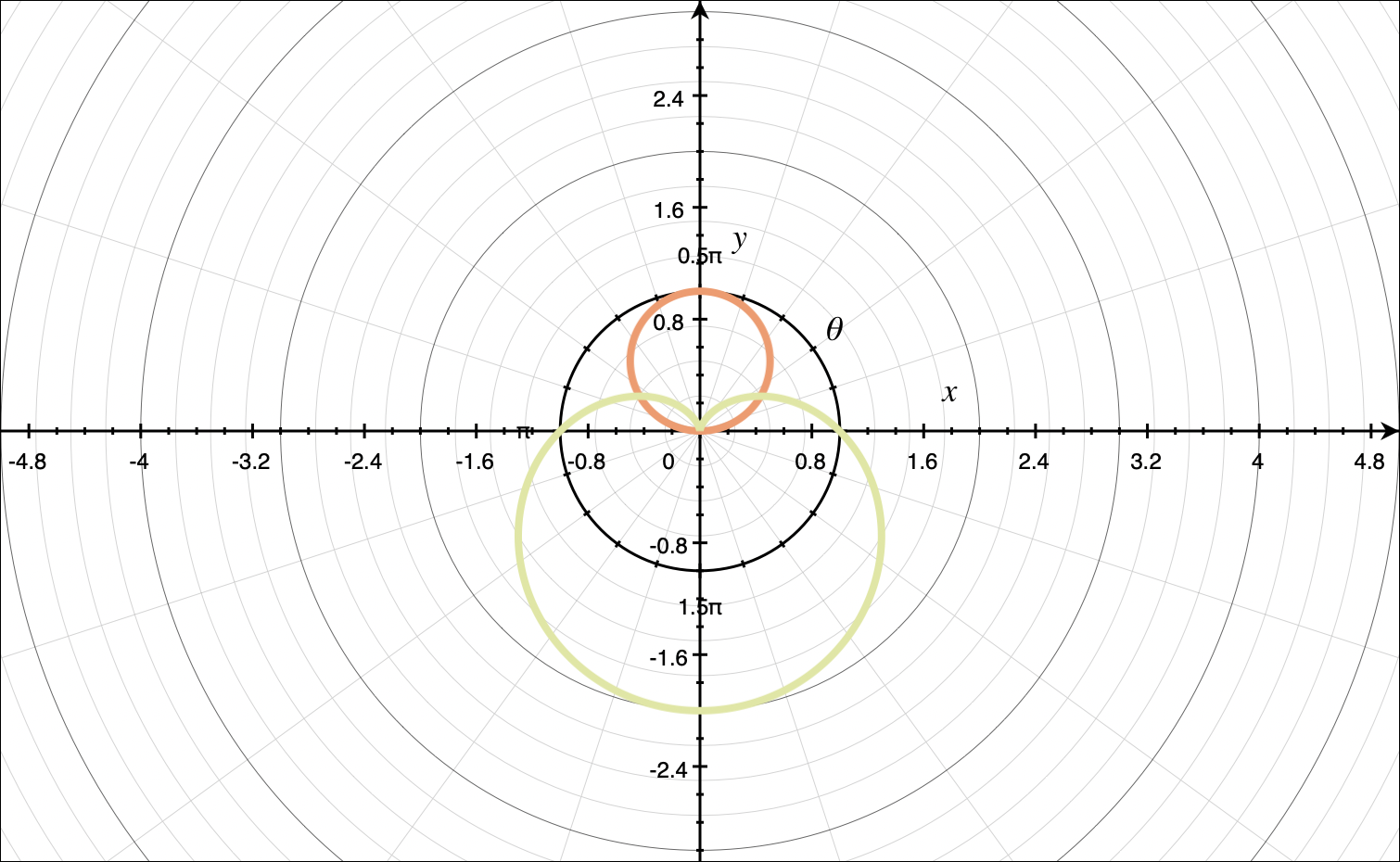
To confirm that these are the points of intersection, we can graph both curves.
Looking at the graph, we see that ???(0,0)??? is also a point of intersection, so in total, the graphs intersect each other at
???\left(\frac12,\frac{\pi}{6}\right)??? and ???\left(\frac12,\frac{5\pi}{6}\right)??? and ???(0,0)???
In the previous example, we had to graph the polar curves in order to find all of the points of intersection. That’s because we left everything in polar form.
Let’s try another example where we convert our polar curves into rectangular coordinates.
Using these steps, we might get more intersection points than actually exist, or fewer intersection points than actually exist.
Example
Find the points of intersection of the polar curves.
???r=\cos{\theta}???
???r=2-\cos{\theta}???
We’ll convert the polar curves to rectangular coordinates using the conversion formula
???x=r\cos{\theta}???
???\cos{\theta}=\frac{x}{r}???
Plugging ???x/r??? into the given polar equations for ???\cos\theta???, we get
???r=\cos{\theta}???
???r=\frac{x}{r}???
???x=r^2???
and
???r=2-\cos{\theta}???
???r=2-\frac{x}{r}???
???x=2r-r^2???
We’ve gotten rid of ???\theta???, but now we need to get rid of ???r???, which we’ll do using the conversion formula
???r^2=x^2+y^2???
???r=\sqrt{x^2+y^2}???
Plugging ???x^2+y^2??? into the given polar equations for ???r^2???, and ???\sqrt{x^2+y^2}??? in for ???r???, we get
???x=r^2???
???x=x^2+y^2???
???x^2+y^2-x=0???
and
???x=2r-r^2???
???x=2\sqrt{x^2+y^2}-\left(x^2+y^2\right)???
???x=2\sqrt{x^2+y^2}-x^2-y^2???
???x^2+y^2-2\sqrt{x^2+y^2}+x=0???
Since both of our rectangular equations are equal to ???0???, we can set them equal to each other.
???x^2+y^2-x=x^2+y^2-2\sqrt{x^2+y^2}+x???
???-x=-2\sqrt{x^2+y^2}+x???
???-2\sqrt{x^2+y^2}=-2x???
???\sqrt{x^2+y^2}=x???
Since we found that ???x^2+y^2=x??? when we were converting ???r=\cos{\theta}??? to rectangular coordinates, we can say
???\sqrt{x}=x???
???x=x^2???
???x^2-x=0???
???x(x-1)=0???
???x=0,\ 1???
To find the ???y???-values associated with these ???x???-values, we’ll plug them into ???x^2+y^2-x=0???.
For ???x=0???:
???(0)^2+y^2-(0)=0???
???y=0???
For ???x=1???:
???(1)^2+y^2-(1)=0???
???y=0???
Putting our values together, we know that the points of intersection are ???(0,0)??? and ???(1,0)???.
We need to convert these rectangular coordinate points back into polar coordinates, which we’ll do using the conversion formulas
???r=\sqrt{x^2+y^2}???
???\theta=\tan^{-1}{\left(\frac{y}{x}\right)}???
Plugging the rectangular coordinate points into these formulas, we get
For ???(0,0)???:
???r=\sqrt{(0)^2+(0)^2}??? so ???r=0???
???\theta=\tan^{-1}{\bigg(\frac{0}{0}\bigg)}???
Since the equation for \theta is undefined, the rectangular point ???(0,0)??? can’t be defined in polar coordinates and therefore isn’t a polar point of intersection.
For ???(1,0)???:
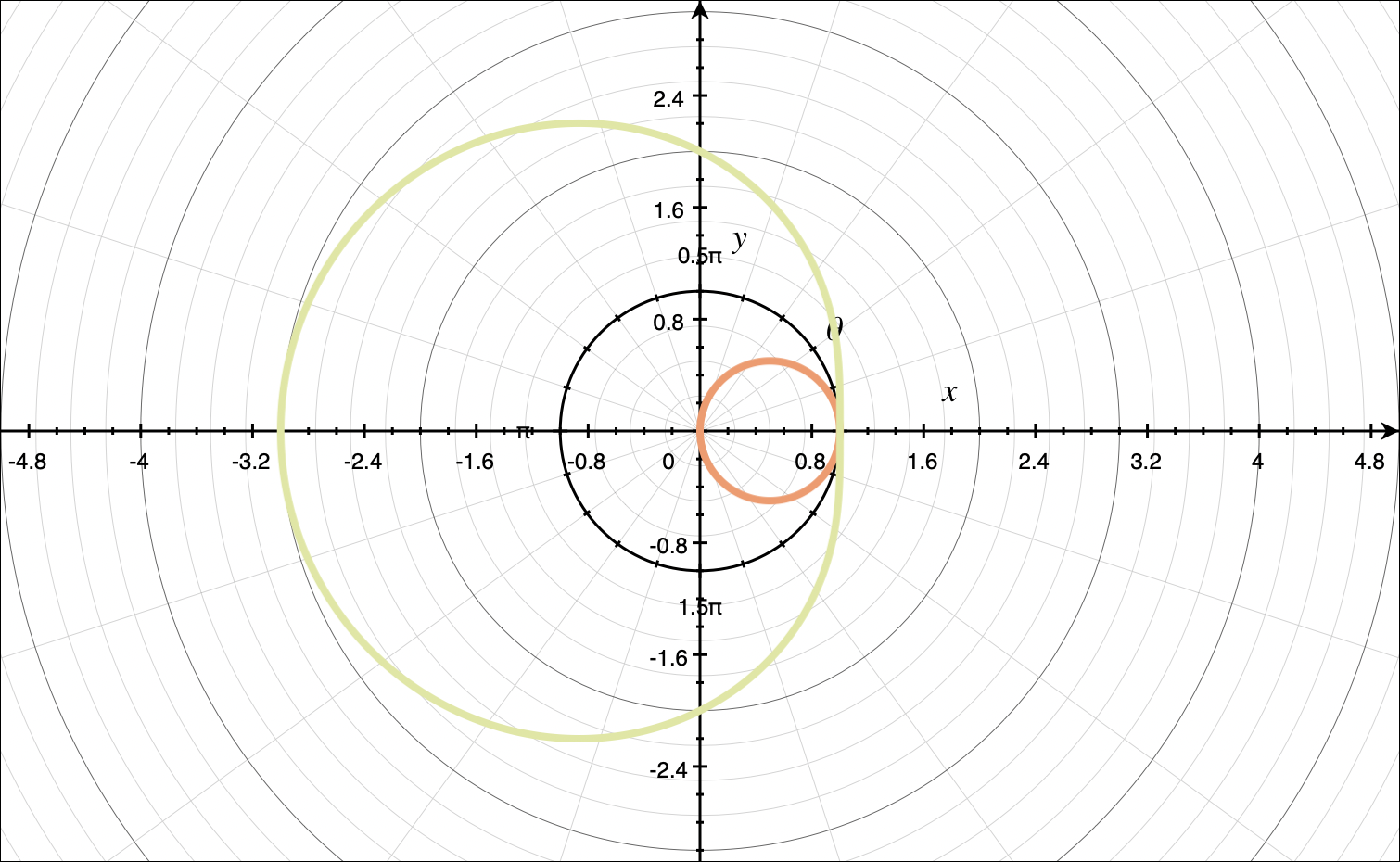
???r=\sqrt{(1)^2+(0)^2}??? so ???r=1???
???\theta=\tan^{-1}{\bigg(\frac{0}{1}\bigg)}??? so ???\theta=0???
The only point of intersection of the given polar curves is the polar point ???(1,0)???. If we want to double-check ourselves, we can sketch the polar curves and confirm this point of intersection.