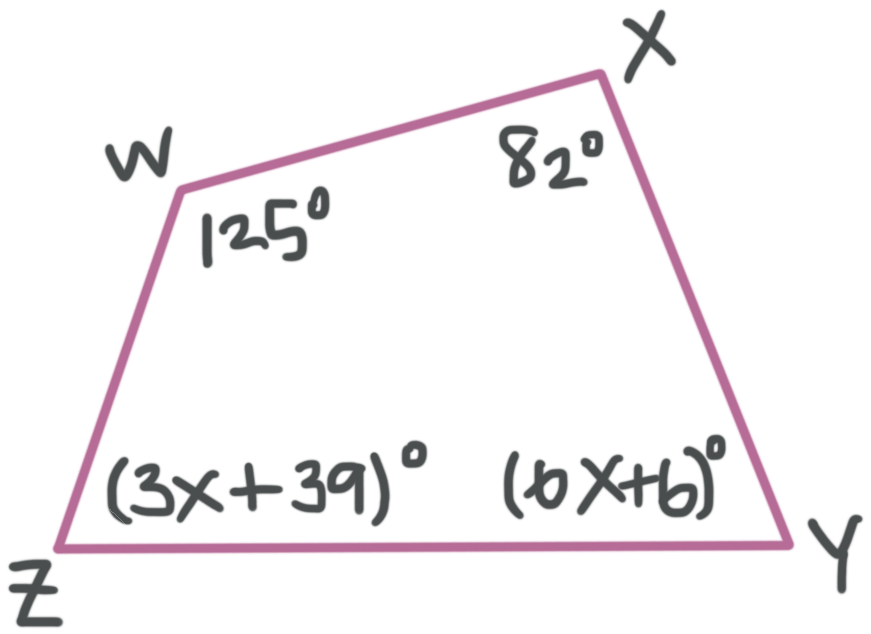Finding interior angles of polygons
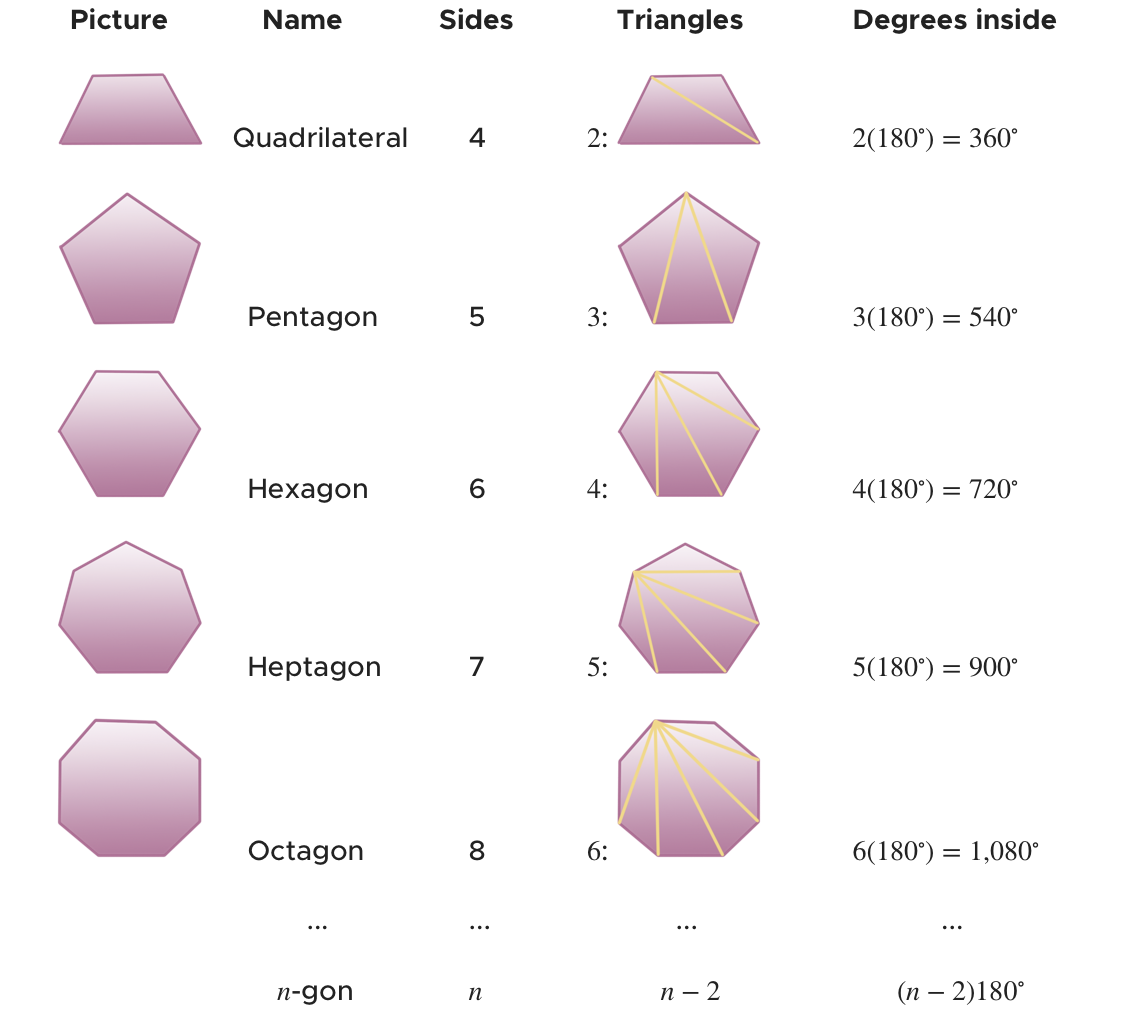
Defining polygons, the number of sides, and the number of interior triangles
In this lesson we’ll look at how to find the measures of the interior angles of polygons by using a formula.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Triangles
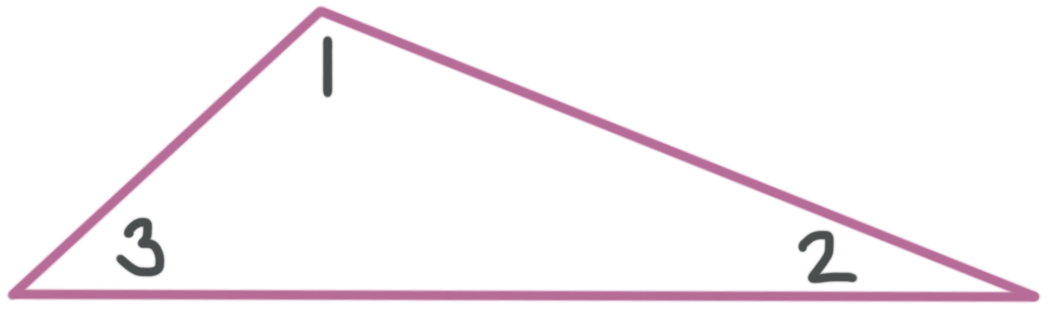
Triangles are ???3???-sided polygons. Remember that the three angles of any type of triangle add up to ???180^\circ???. For instance, in this figure, ???m\angle1+m\angle2+m\angle3=180^\circ???.
Polygons
The word “polygon” means “many-sided figure.” A polygon has the same number of angles as it has sides, and a regular polygon has equal angles and equal sides.
Any polygon can be divided into triangles.
How to solve for the measures of the interior angles of a triangle
Take the course
Want to learn more about Geoemtry? I have a step-by-step course for that. :)
Measures of the interior angles of regular and irregular polygons
Example
What is the measure of each individual angle in a regular icosagon (a ???20???-sided figure)?
The sum of the angles in a polygon is ???(n-2)180^\circ???, where ???n??? is the number of sides in the polygon. For an icosagon, which is a ???20???-sided figure, that would be
???(20-2)180^\circ =3,240^\circ???
There are ???20??? congruent interior angles because the shape is regular, so each interior angle measures
???3,240^\circ \div 20=162^\circ???
If the shape is not regular then you can’t assume all of the angles are congruent. Let’s look at an example with non-regular interior angles.
If the shape is not regular then you can’t assume all of the angles are congruent.
Example
What is the measure of ???\angle Z????
The sum of the angles in a polygon is ???(n-2)180^\circ???. For a quadrilateral, that would be ???(4-2)180^\circ =360^\circ???. Set the sum of the four angles equal to ???360^\circ??? and then solve for ???x???.
???125^\circ +82^\circ +3x+39^\circ +6x+6^\circ =360^\circ???
???252^\circ +9x=360^\circ???
???9x=108^\circ???
???x=12^\circ???
Substitute ???12^\circ??? for ???x??? in ???(3x+39)^\circ??? to find ???m\angle Z???.
???m\angle Z=(3\cdot 12+39)^\circ =75^\circ???