Solving for the interior angles of a triangle
Every triangle has three interior angles
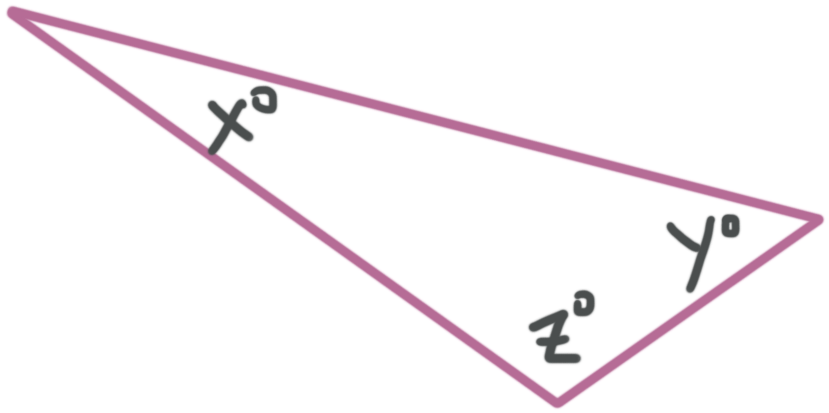
The interior angles of a triangle are the three angles on the inside of a triangle. These three angles always sum to ???180{}^\circ???.
???x{}^\circ +y{}^\circ +z{}^\circ =180{}^\circ???
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
There are a few other angle relationships we need to remember:
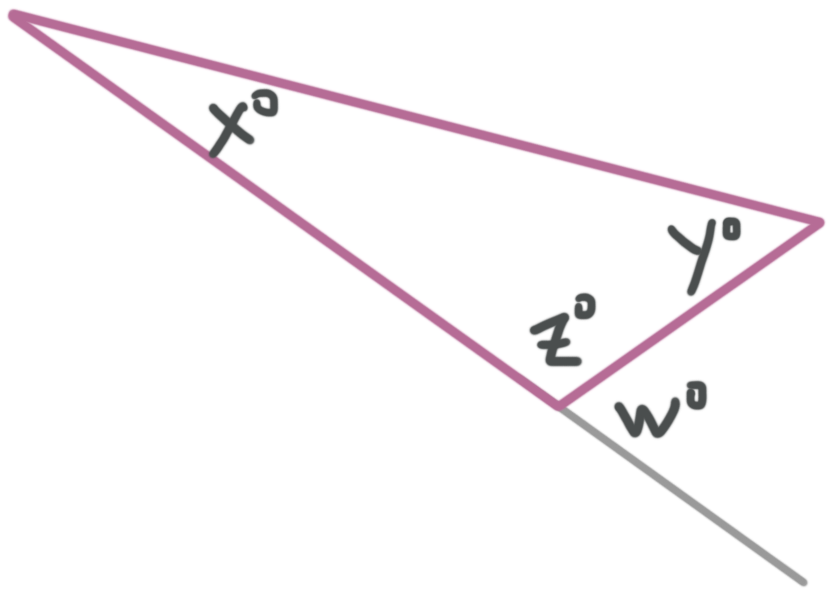
The angle measures that form a straight line add to ???180^\circ???, so ???z^\circ+w^\circ=180^\circ???.
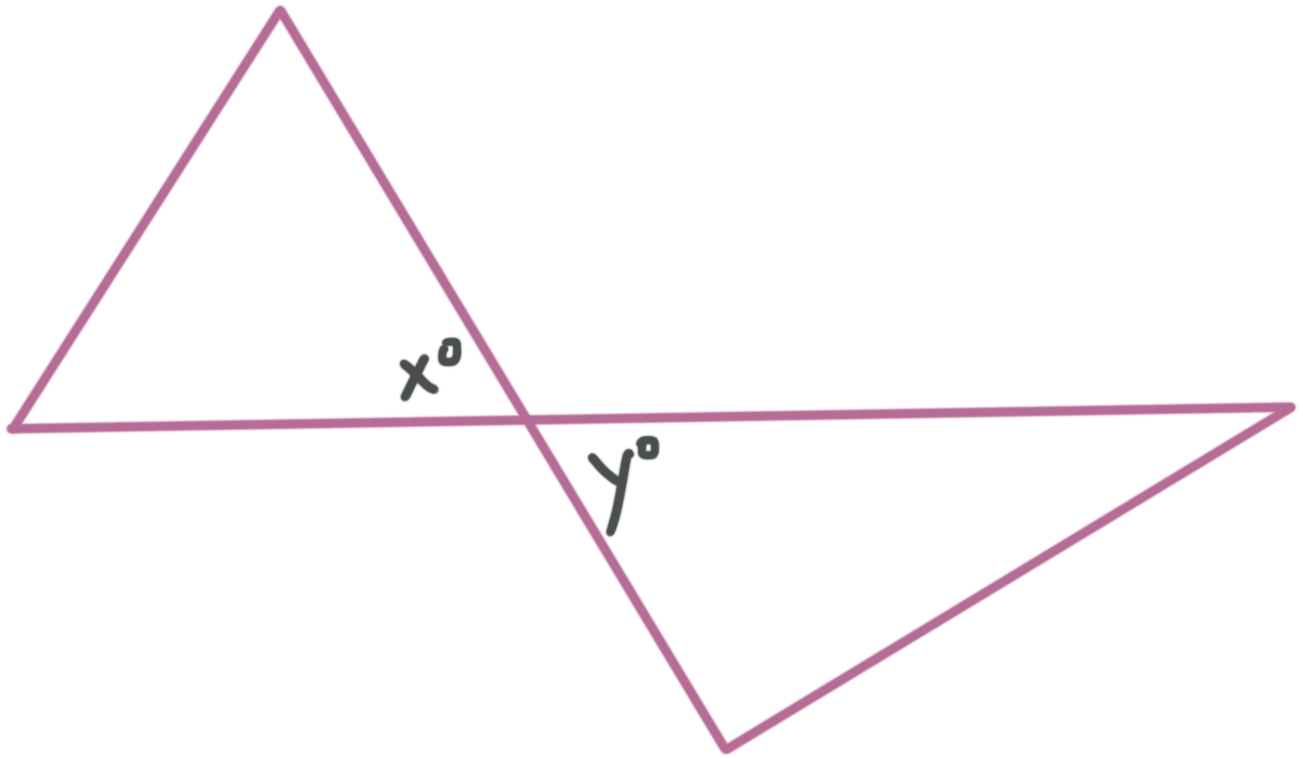
Vertical angles are congruent, so ???x^\circ=y^\circ???.
How to determine whether the set of angles creates a triangle
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Finding the unknown exterior angle of a triangle
Let’s start by working through an example.
Example
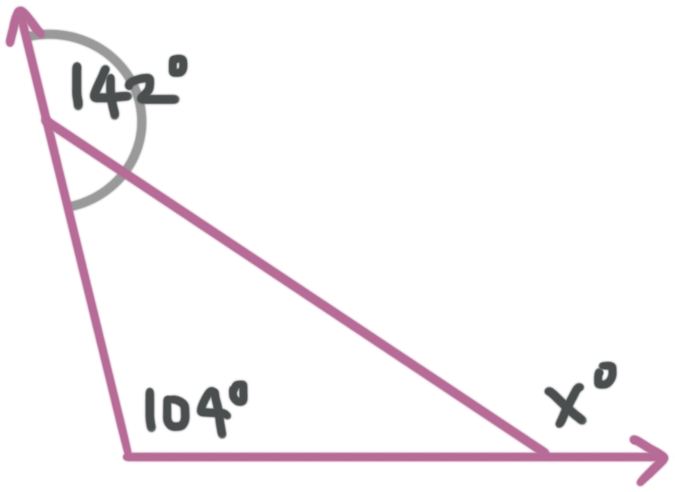
What is the value of ???x????
We know that these two angles lie on a straight line:
We can find the measure of the angle by subtracting ???180{}^\circ -142{}^\circ =38{}^\circ???.
The three angles inside a triangle sum to ???180{}^\circ???, so
???180{}^\circ -104{}^\circ -38{}^\circ =38{}^\circ???
Now we can see that ???x^\circ??? and ???38^\circ??? lie on a straight line, so
???x{}^\circ +38{}^\circ =180{}^\circ???
???x{}^\circ =142{}^\circ???
Let’s try another one.
The interior angles of a triangle are the three angles on the inside of a triangle. These three angles always sum to 180 degrees.
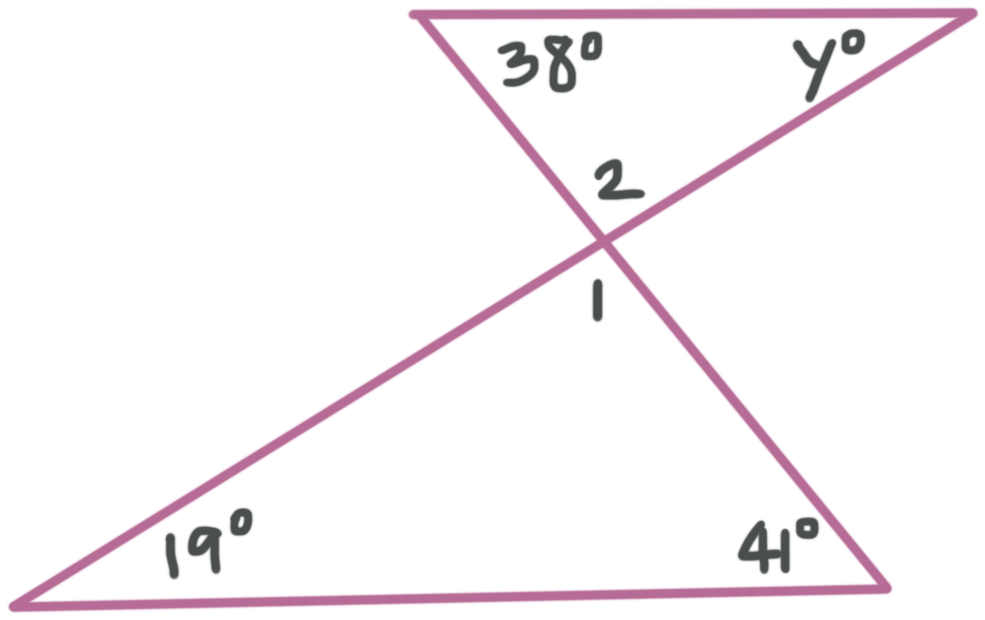
Example
What is the value of ???y????
The three interior angles of a triangle sum to ???180{}^\circ???, so
???m\angle 1+19{}^\circ +41{}^\circ =180{}^\circ???
???m\angle 1=120{}^\circ???
Vertical angles are congruent, so
???m\angle 1=m\angle 2=120{}^\circ???
Again, the three angles of a triangle sum to ???180{}^\circ???, so we can say
???m\angle 2+38^\circ +y^\circ =180^\circ???
???120^\circ +38^\circ +y^\circ =180^\circ???
???y^\circ =22^\circ???