Finding infinite limits at vertical asymptotes
Limits at infinity vs. infinite limits
There’s a difference between “limits at infinity” and “infinite limits.” When we see limits at infinity, it means we’re talking about the limit of the function as we approach ???\infty??? or ???-\infty???. Contrast that with infinite limits, which means that the value of the limit is ???\infty??? or ???-\infty??? as we approach a particular point.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Limits at infinity, infinite limits
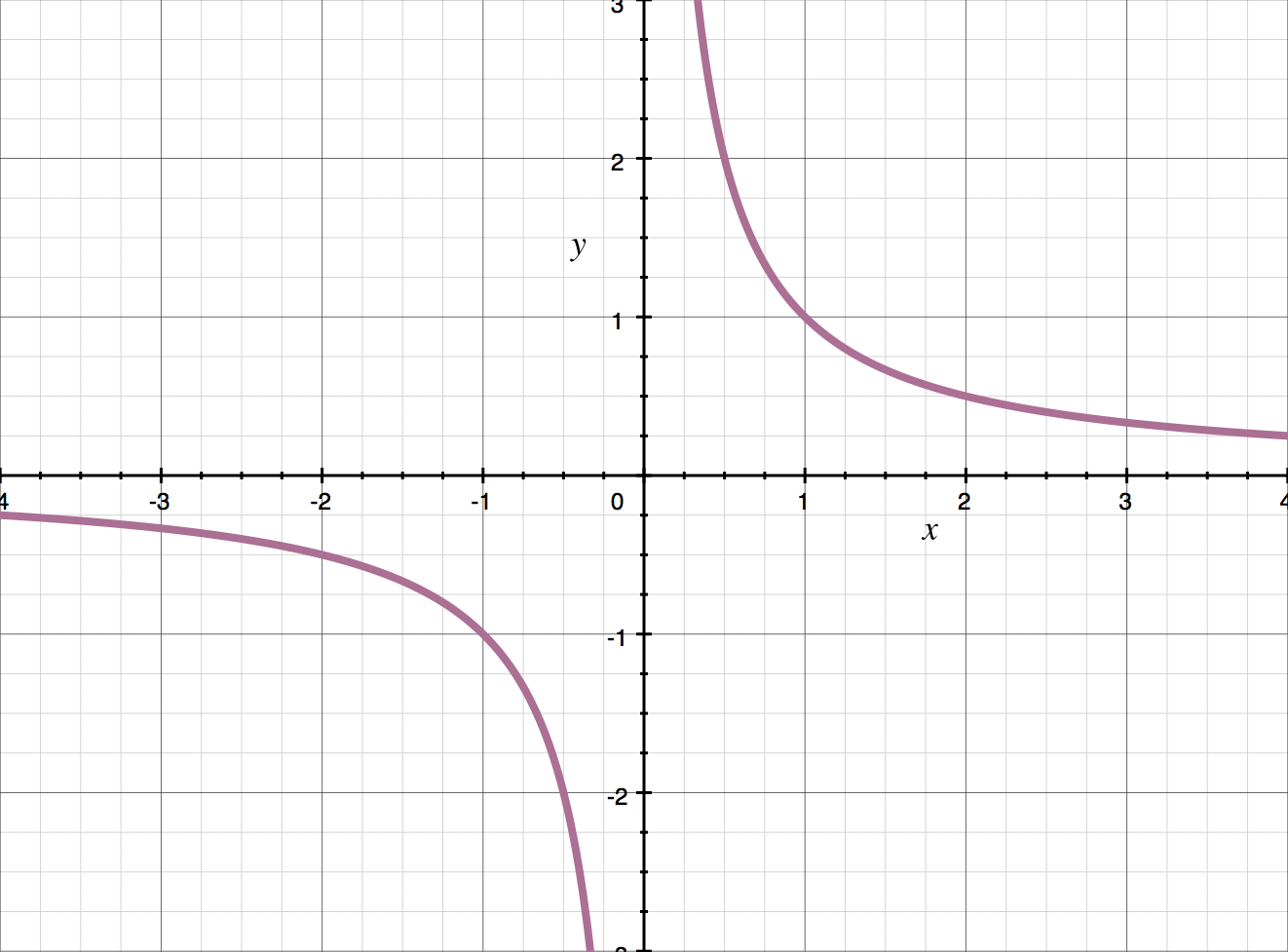
In the graph of ???f(x)=1/x???,
the function has infinite, one-sided limits at ???x=0???. There’s a vertical asymptote there, and we can see that the function approaches ???-\infty??? from the left, and ???\infty??? from the right.
???\lim_{x\to0^-}\frac{1}{x}=-\infty???
???\lim_{x\to0^+}\frac{1}{x}=\infty???
Talking about limits at infinity for this function, we can see that the function approaches ???0??? as we approach either ???\infty??? or ???-\infty???.
???\lim_{x\to-\infty}\frac{1}{x}=0???
???\lim_{x\to\infty}\frac{1}{x}=0???
How to find infinite limits
Infinite limits exist around vertical asymptotes in the function. Of course, we get a vertical asymptote whenever the denominator of a rational function in lowest terms is equal to ???0???.
Here’s an example of a rational function in lowest terms, meaning that we can’t factor and cancel anything from the fraction.
???\lim_{x\to1}\frac{1}{(x-1)^2}???
We can see that setting ???x=1??? gives ???0??? in the denominator, which means that we have a vertical asymptote at ???x=1???. Therefore, we know we’ll have infinite limits on either side of ???x=1???.
Once we’ve established that this is a rational function in lowest terms and that a vertical asymptote exists, all that’s left to determine is whether the one-sided limits around ???x=1??? approach ???\infty??? or ???-\infty???.
In order to do that, we can substitute values very close to ???x=1???. If the result is positive, the limit will be ???\infty???; if the result is negative, the limit will be ???-\infty???.
???f(0.99)=\frac{1}{(0.99-1)^2}=\frac{1}{(-0.01)^2}=\frac{1}{0.0001}=10,000=\infty???
???f(1.01)=\frac{1}{(1.01-1)^2}=\frac{1}{(0.01)^2}=\frac{1}{0.0001}=10,000=\infty???
Because the value of the function tends toward ???\infty??? on both sides of the vertical asymptote, we can say that the general limit of the function as ???x\to1??? is ???\infty???.
???\lim_{x\to1}\frac{1}{(x-1)^2}=\infty???