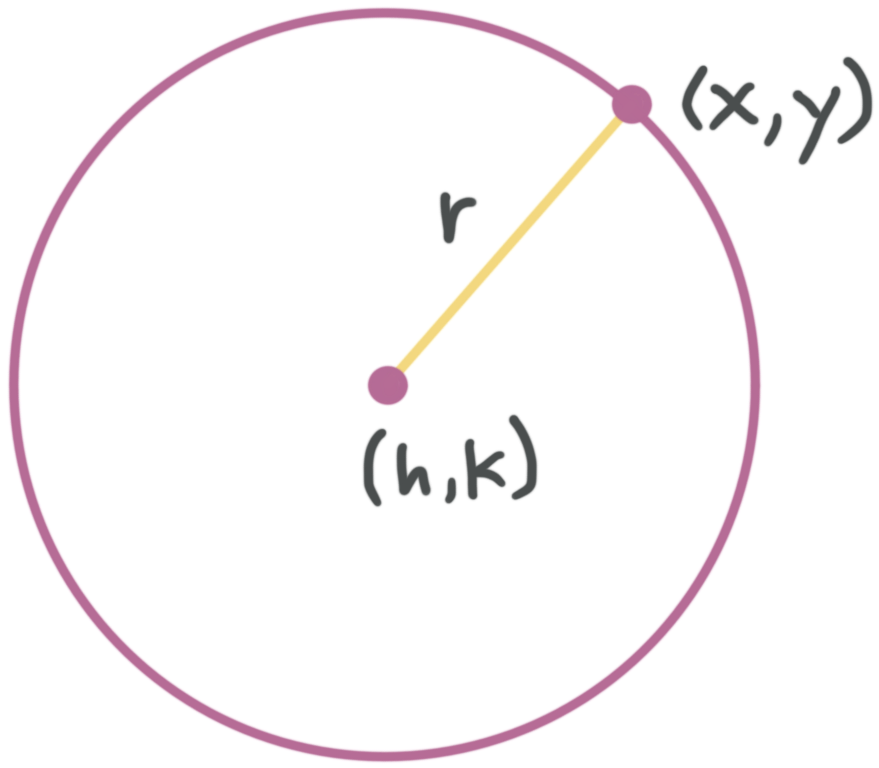How to find the equation of a circle
Formula for the equation of a circle
In this lesson we’ll look at the equation for a circle, ???{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}???, and how to use it to graph a circle, interpret points on a circle and write an equation given a graph or the special features of a circle.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
A circle can be defined by a center point and a radius of a certain length. In the equation of a circle
???{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}???
the center is called ???(h,k)??? and the radius is ???r???. From the equation, you can see that the circle is the collection of all the ???(x,y)??? points that are a distance ???r??? from the center, ???(h,k)???.
The collection of ???(x,y)??? values are the points on the circle’s circumference.
How to find the equation of a circle, given different information about the circle
Take the course
Want to learn more about Geoemtry? I have a step-by-step course for that. :)
Let’s work through four different examples of how to find the equation of a circle
Example
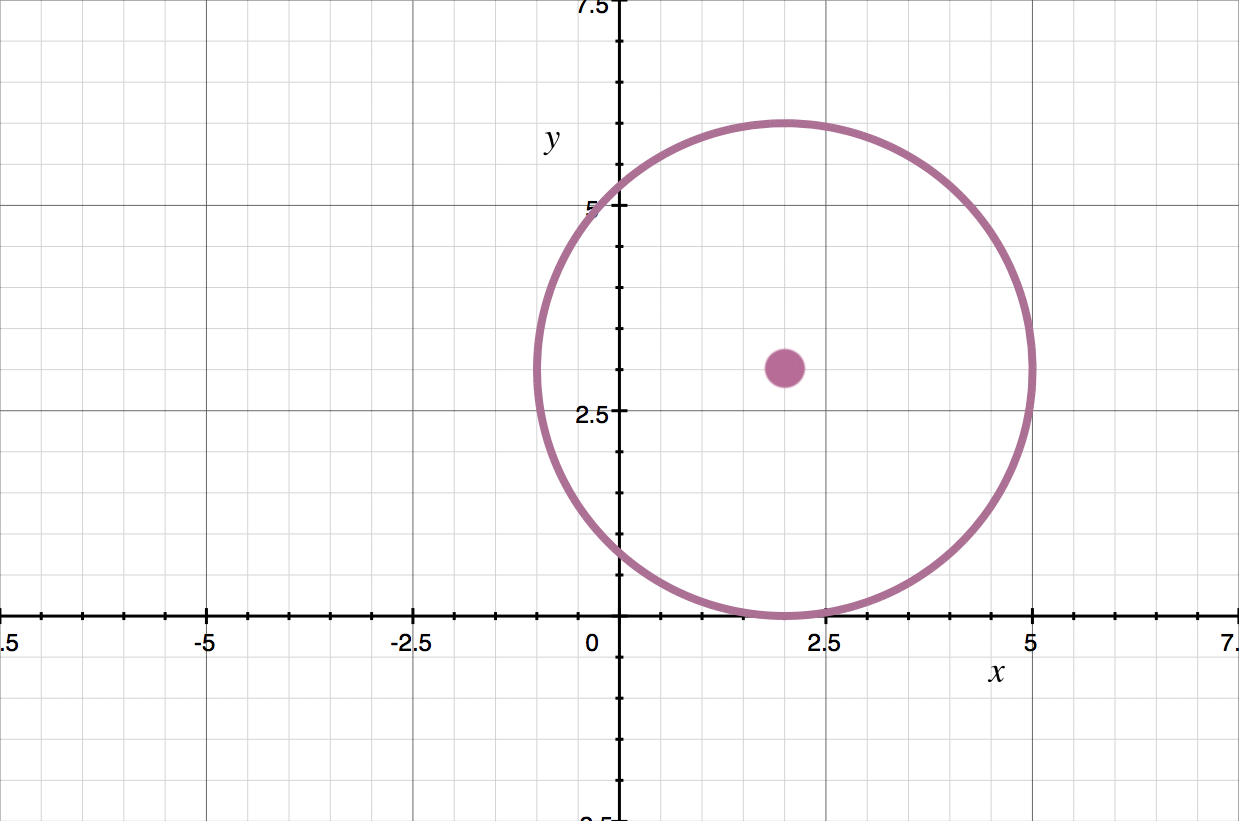
What is the equation of the circle?
We need to find the equation of a circle in the form ???(x-h)^2+(y-k)^2=r^2???, which means we need to find the center point and the length of the radius.
The center is at ???(2,3)???, so ???h=2??? and ???k=3???.
Now let’s count from the center to a point on the circumference to find the length of the radius.
The radius is ???3??? so ???r=3???. Now let’s plug everything into the standard form of a circle.
???(x-2)^2+(y-3)^2=3^2???
???(x-2)^2+(y-3)^2=9???
Sometimes we want to know the center and radius of a circle given the equation of the circle.
Example
What is the center and radius of the circle?
???{{x}^{2}}+{{(y-3)}^{2}}=27???
We can rewrite the equation as
???{{(x-0)}^{2}}+{{(y-3)}^{2}}=27???
Which lets us identify ???h=0??? and ???k=3???, so the center is at ???(0,3)???. And the radius is then ???\sqrt{27}???, so
???r=\sqrt{27}???
???r=\sqrt{9\cdot 3}???
???r=\sqrt{9}\cdot \sqrt{3}???
???r=3\sqrt{3}???
Sometimes we want to know the -intercepts of a circle.
A circle can be defined by a center point and a radius of a certain length.
Example
What are the ???x???-intercepts of the circle?
???{{(x-2)}^{2}}+{{(y+1)}^{2}}=16???
At the ???x???-intercepts, ???y=0???, so let ???y??? be ???0???, and rewrite the equation.
???{{(x-2)}^{2}}+{{(y+1)}^{2}}=16???
???{{(x-2)}^{2}}+{{(0+1)}^{2}}=16???
???{{(x-2)}^{2}}+1^2=16???
???{{x}^{2}}-4x+4+1=16???
???{{x}^{2}}-4x+5=16???
???{{x}^{2}}-4x-11=0???
If you can’t factor the equation to solve for ???x??? you can use the quadratic formula. In this case, ???a=1???, ???b=-4???, and ???c=-11???.
???x=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}???
???x=\frac{4\pm \sqrt{{{(-4)}^{2}}-4(1)(-11)}}{2(1)}???
???x=\frac{4\pm \sqrt{60}}{2}=\frac{4\pm \sqrt{4\cdot 15}}{2}=\frac{4\pm 2\sqrt{15}}{2}=2\pm \sqrt{15}???
These are the ???x???-intercepts.
Sometimes to find out information about a circle you’ll need to know how to complete the square.
Example
Find the center and radius of the circle.
???x^2+y^2+24x+10y+160=0???
In order to find the center and radius, we need to change the equation of the circle into standard form, ???(x-h)^2+(y-k)^2=r^2???. In order to get the equation into standard form, we have to complete the square with respect to both variables.
Grouping ???x???’s and ???y???’s together and moving the constant to the right side, we get
???(x^2+24x)+(y^2+10y)=-160???
Completing the square requires us to take the coefficient on the first degree terms, divide them by ???2???, then square the result before adding the result back to both sides.
The coefficient on the ???x??? term is ???24???, so
???\frac{24}{2}=12\quad\rightarrow\quad12^2=144???
The coefficient on the ???y??? term is ???10???, so
???\frac{10}{2}=5\quad\rightarrow\quad5^2=25???
So we add ???144??? inside the parentheses with the ???x??? terms, ???25??? inside the parenthesis with the ???y??? terms and also add ???144??? and ???25??? to the right side with the ???-160???.
???(x^2+24x +144)+(y^2+10y+25)=-160 + 144+25???
???(x+12)^2+(y+5)^2=9???
Therefore, the center of the circle is at ???(h,k)=(-12,-5)??? and its radius is ???r=\sqrt{9}=3???.
