Distance between two points in three dimensions
Plotting points in three dimensions
In this lesson we’ll look at points that are plotted three-dimensionally and how to find the distance between them.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
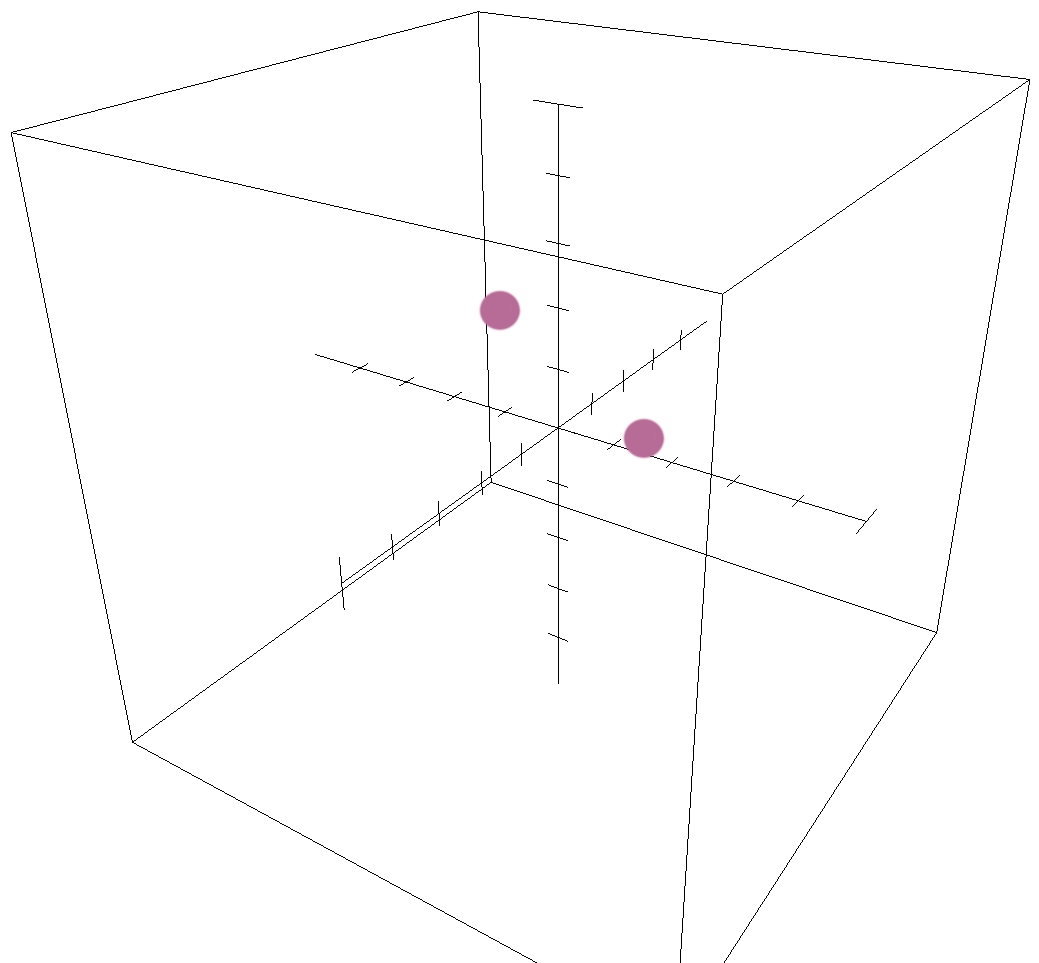
Points
A point is a representation of a location in space. Its symbol is a single letter, and it’s represented as a dot. When we’re talking about a three-dimensional point, we have three locations: the ???x???-axis, the ???y???-axis and the ???z???-axis. So a point is represented as ???(x,y,z)???. Here are two points ???A??? and ???B??? plotted in three-dimensional space:
Distance formula
We can use the distance formula for three dimensions to find the length of the line segment that connects two points in three-dimensional space.
???d=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}+{{({{z}_{1}}-{{z}_{2}})}^{2}}}???
where ???{{P}_{1}}=({{x}_{1}},{{y}_{1}},{{z}_{1}})??? and ???{{P}_{2}}=({{x}_{2}},{{y}_{2}},{{z}_{2}})???.
Simplifying radicals
Since the distance formula takes the square root of a series of operations, it can be useful to know how to simplify radicals. Remember when you simplify a radical, that the radical has to have no perfect squares remaining under the radical symbol. For example,
???\sqrt{18}=\sqrt{9\cdot 2}=\sqrt{9}\cdot \sqrt{2}=3\sqrt{2}???
Finding the distance between two points in three-dimensional space
Take the course
Want to learn more about Geoemtry? I have a step-by-step course for that. :)
Calculate the distance between the points
Example
Calculate the distance between Points ???B??? and ???C???.
???B=(4,-5,8)???
???C=(1,-3,2)???
We need to use the distance formula.
???d=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}+{{({{z}_{1}}-{{z}_{2}})}^{2}}}???
???d=\sqrt{{{(4-1)}^{2}}+{{(-5-(-3))}^{2}}+{{(8-2)}^{2}}}???
???d=\sqrt{{{(3)}^{2}}+{{(-2)}^{2}}+{{(6)}^{2}}}???
???d=\sqrt{9+4+36}???
???d=\sqrt{49}???
???d=7??? units
Now let’s try one where we’ll need to simplify the radical.
We can use the distance formula for three dimensions to find the length of the line segment that connects two points in three-dimensional space.
Example
Calculate the distance between Points ???A??? and ???D???.
???A=(3,9,-2)???
???D=(0,-5,4)???
We need to use the distance formula.
???d=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}+{{({{z}_{1}}-{{z}_{2}})}^{2}}}???
???d=\sqrt{{{(3-0)}^{2}}+{{(9-(-5))}^{2}}+{{(-2-4)}^{2}}}???
???d=\sqrt{{{(3)}^{2}}+{{(14)}^{2}}+{{(-6)}^{2}}}???
???d=\sqrt{9+196+36}???
???d=\sqrt{241}\approx15.5??? units