Finding the diagonal of a right rectangular prism
Formula for the diagonal in terms of the length, width, and height of the rectangular prism
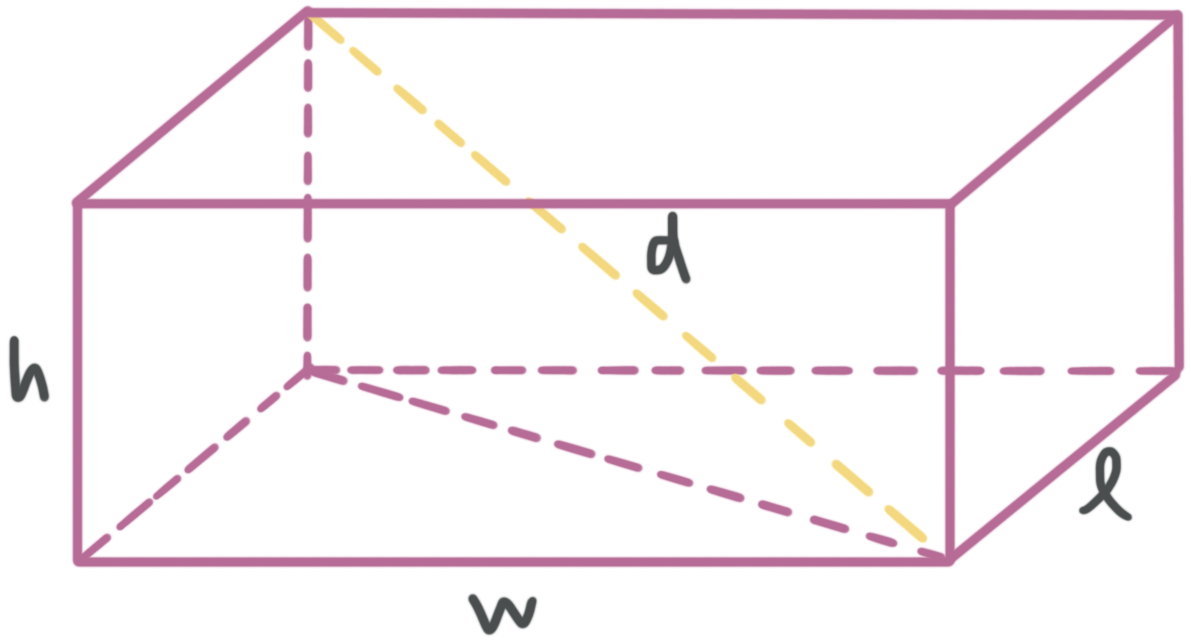
The diagonal of a right rectangular prism goes from one corner of the prism, across the interior volume, all the way to the opposite corner of the prism.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
You can find the length of a diagonal of a right rectangular prism using
???d=\sqrt{{{l}^{2}}+{{w}^{2}}+{{h}^{2}}}???
where ???d??? is the length of the diagonal, and ???l???, ???w???, and ???h??? are the length, width, and height, respectively.
How to find the length of the diagonal
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Length of the diagonal of a right rectangular prism
Example
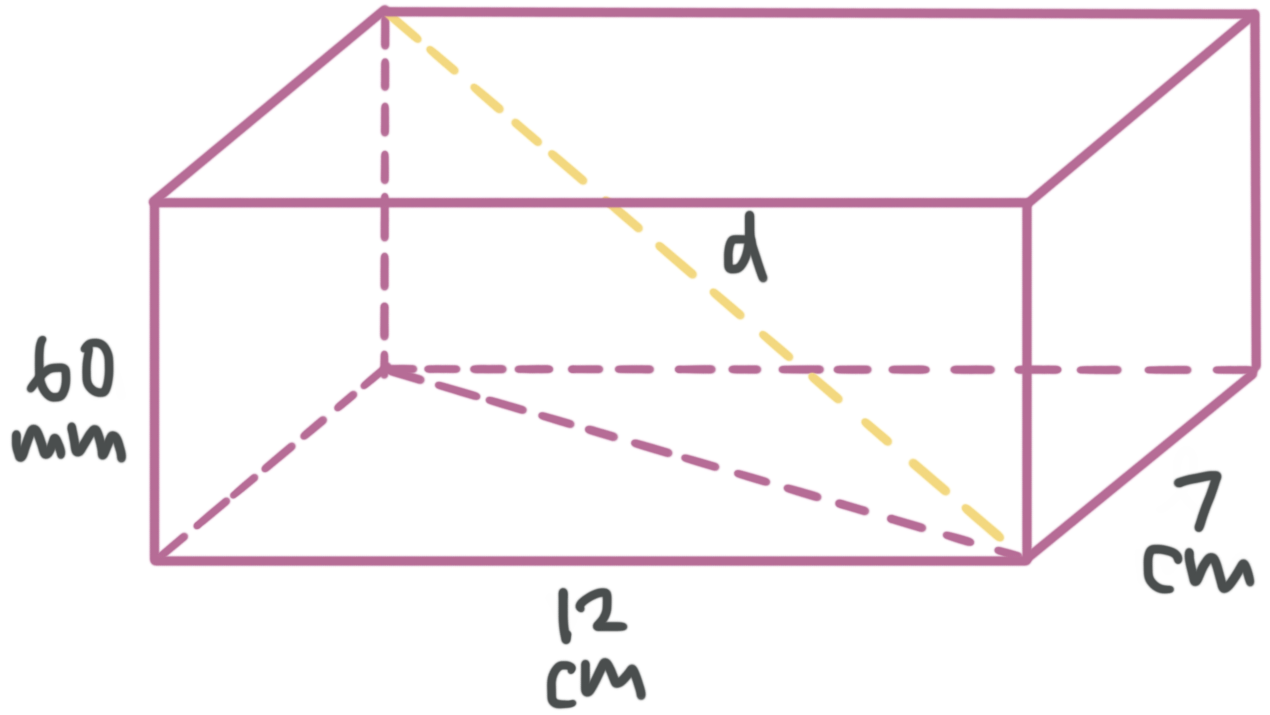
What is the length of the diagonal of the right rectangular prism?
Not all of the dimensions here are the same. Change ???60\text{ mm}??? to centimeters first.
???60\text{ mm}=6\text{ cm}???
Then the dimensions are
Plugging these into the formula for the diagonal, we get
???d=\sqrt{{{l}^{2}}+{{w}^{2}}+{{h}^{2}}}???
???d=\sqrt{{{7}^{2}}+{{12}^{2}}+{{6}^{2}}}???
???d=\sqrt{49+144+36}???
???d=\sqrt{229}??? cm
Let’s try another one.
The diagonal of a right rectangular prism goes from one corner of the prism, across the interior volume, all the way to the opposite corner of the prism.
Example
Find the width of the right rectangular prism.
We just need to plug the dimensions we’ve been given into the formula for the diagonal.
???d=\sqrt{{{l}^{2}}+{{w}^{2}}+{{h}^{2}}}???
???7\sqrt{2}=\sqrt{{{5}^{2}}+{{w}^{2}}+{{3}^{2}}}???
Manipulate the equation to solve for ???w???.
???(49)(2)={{5}^{2}}+{{w}^{2}}+{{3}^{2}}???
???98=25+{{w}^{2}}+9???
???98=34+{{w}^{2}}???
???64={{w}^{2}}???
???8=w???