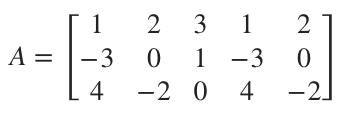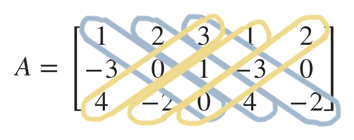All about the determinant of a matrix

Defining the determinant for 2x2 and 3x3 matrices

In previous lessons, we learned two ways to find the inverse matrix. The first way was to augment the ???n\times n??? matrix with the ???I_n??? identity matrix, and then put the matrix into reduced row-echelon form. Doing so changes the augmented ???I_n??? matrix into the inverse matrix.

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

The second way was to plug into the inverse matrix formula that uses the determinant,

In this lesson, we want to dig more into the determinant, both for a ???2\times2??? matrix, and for larger matrices as well.

The determinant for ???2\times2??? matrices

First, let’s talk more about the formula for the inverse matrix,

We want to notice one really important thing. The inverse matrix is not defined when ???ad-bc=0???. In other words, if ???ad-bc=0???, then we get a ???0??? in the denominator of the fraction in the formula, which means the fraction is undefined, which means the inverse matrix itself is undefined.

And this fact actually becomes extremely useful for us. Because now we have a test that we can use to determine whether or not a matrix is invertible.

As we’ve said, the denominator ???ad-bc??? is called the determinant of the matrix. So we can simply calculate the determinant, and then

if the determinant is ???0???, the matrix is not invertible, so you can’t find its inverse, but
if the determinant is nonzero, the matrix is invertible, so you can find its inverse.

We write the determinant of the matrix

as any of these:

The determinant for ???3\times3??? and ???n\times n??? matrices

And the determinant isn’t only for ???2\times2??? matrices. We have a formula for the determinant of a ???3\times3??? formula as well.

Given a matrix

its determinant is

Notice how the determinant with ???a??? includes all of the entries outside of the row and column that contain ???a??? in the ???3\times3??? determinant.

In the same way, the determinant with ???b??? includes all of the entries outside of the row and column that contain ???b???,

and the determinant with ???c??? includes all of the entries outside of the row and column that contain ???c???.

This will always be how we’ll calculate the determinant.

Notice also then that what’s left in this ???3\times3??? determinant formula are a few ???2\times2??? determinants. We know how to calculate their determinants already, so we can simplify this formula even further.

???|A|=a(ei-fh)-b(di-fg)+c(dh-eg)???

???|A|=aei-afh-bdi+bfg+cdh-ceg???

???|A|=aei+bfg+cdh-afh-bdi-ceg???

We can expand this process beyond ???2\times2??? and ???3\times3??? matrices, to any ???n\times n??? matrix. You may have noticed in the formula for the ???3\times3??? determinant that we alternated signs, starting with a positive sign, and we got ???+a???, then ???-b???, then ???+c???. The formula for an ???n\times n??? matrix will always follow this same ???+,\ -, +,\ -,\ ...??? pattern.

And the formula for an ???n\times n??? matrix is recursive. In the same way that the formula the ???3\times3??? determinant reduced the ???3\times3??? determinant to a set of ???2\times2??? determinants, the ???n\times n??? determinant formula will reduce the ???n\times n??? determinant to a set of ???(n-1)\times (n-1)??? determinants, which can then be reduced to a set of ???(n-2)\times (n-2)??? determinants, and so on, until eventually you’ll be left with only a set of ???2\times2??? determinants, which can be evaluated directly as ???ad-bc???.

The following is true for the ???n\times n??? matrices as well.

if the determinant is ???0???, the matrix is not invertible, so you can’t find its inverse, but
if the determinant is nonzero, the matrix is invertible, so you can find its inverse.

Finding the determinant for any size matrix

Take the course

Want to learn more about Linear Algebra? I have a step-by-step course for that. :)

Learn More

Finding the determinant for a 4x4 matrix

Let’s do an example to make sure we know how to use this method for a larger matrix.

Example

Use the determinant to say whether the matrix ???A??? is invertible.

The matrix ???A??? is ???4\times 4???. Which means we’ll find its determinant by reducing to a set of ???3\times 3??? determinants with alternating signs,

and then to a set of ???2\times 2??? determinants with alternating signs.

Now that we have only ???2\times2??? determinants remaining, we can evaluate using the ???ad-bc??? pattern.

???|A|=1\left[0((0)(-1)-(3)(2))-1((-2)(-1)-(3)(1))+2((-2)(2)-(0)(1))\right]???

???-2\left[-3((0)(-1)-(3)(2))-1((4)(-1)-(3)(4))+2((4)(2)-(0)(4))\right]???

???+3\left[-3((-2)(-1)-(3)(1))-0((4)(-1)-(3)(4))+2((4)(1)-(-2)(4))\right]???

???-4\left[-3((-2)(2)-(0)(1))-0((4)(2)-(0)(4))+1((4)(1)-(-2)(4))\right]???

???|A|=1\left[0(0-6)-1(2-3)+2(-4-0)\right]???

???-2\left[-3(0-6)-1(-4-12)+2(8-0)\right]???

???+3\left[-3(2-3)-0(-4-12)+2(4+8)\right]???

???-4\left[-3(-4-0)-0(8-0)+1(4+8)\right]???

???|A|=1\left[0(-6)-1(-1)+2(-4)\right]-2\left[-3(-6)-1(-16)+2(8)\right]???

???+3\left[-3(-1)-0(-16)+2(12)\right]-4\left[-3(-4)-0(8)+1(12)\right]???

???|A|=1(0+1-8)-2(18+16+16)+3(3-0+24)-4(12-0+12)???

???|A|=1(-7)-2(50)+3(27)-4(24)???

???|A|=-7-100+81-96???

???|A|=-122???

Because the determinant is nonzero, we know that ???A??? is invertible, which means we’ll be able to find its inverse.

Because the determinant is nonzero, we know that the matrix is invertible, which means we’ll be able to find its inverse.

The determinant along different rows and columns

So far, we’ve been calculating determinants by focusing on the first row of the matrix. In other words, for the matrix

from the last example, we used the coefficients with alternating signs from the first row, ???+1???, ???-2???, ???+3???, and ???-4???, and multiplied them by their associated sub-matrices as determinants.

But we don’t have to use the first row. We can actually use any row or any column that we choose, and we’ll always get the same value for the determinant. The benefit of this flexibility is that we can try to choose rows that have the most zero values, to make our calculation simpler.

For instance, with the matrix ???A???, let’s find the determinant along the second row, since the second row includes a ???0???. We just need to remember the checkerboard pattern of positive and negative signs. The entry in the first column of the first row is positive, and then everything alternates from there:

So the determinant of ???A??? along the second row would be

Using the second row means that the second term in ???|A|??? will be zeroed out.

Now for the first term, we’ll find the determinant along the second row, since it includes a ???0???. We could just as easily use second column, which also includes the same ???0???, but we’ll do the row again.

The ???0??? cancels out the second term completely.

We’ll find the determinant along the first row for the next determinant, since there are no zeros in the matrix, but we’ll find the determinant along the third column for the last determinant (we could just as easily find it along the second row, which includes the same ???0???). Remember the checkerboard sign pattern.

The ???0??? from that third column will zero out the second term.

Now, with a simplified equation, we can more quickly calculate the determinant, and we’ll get the same value we did before when we always used the first row.

???|A|=3\left[2((3)(-1)-(4)(2))-3((2)(2)-(3)(1))\right]???

???-1\left[1((-2)(-1)-(3)(1))-2((4)(-1)-(3)(4))+4((4)(1)-(-2)(4))\right]???

???+2\left[3((4)(1)-(-2)(4))+2((1)(-2)-(2)(4))\right]???

???|A|=3\left[2(-3-8)-3(4-3)\right]???

???-1\left[1(2-3)-2(-4-12)+4(4+8)\right]???

???+2\left[3(4+8)+2(-2-8)\right]???

???|A|=3\left[2(-11)-3(1)\right]-1\left[1(-1)-2(-16)+4(12)\right]+2\left[3(12)+2(-10)\right]???

???|A|=3(-22-3)-1(-1+32+48)+2(36-20)???

???|A|=3(-25)-1(79)+2(16)???

???|A|=-75-79+32???

???|A|=-122???

This is the same result as the one we got when we always found the determinant along the first row, despite the fact that, this time, we chose different rows and columns along which to calculate the determinant.

The determinant by the Rule of Sarrus

Remember before that we found the determinant of the ???3\times3??? matrix

to be

???|A|=aei+bfg+cdh-afh-bdi-ceg???

But instead of remembering this formula, the Rule of Sarrus tells us that each of these terms (???aei???, ???bfg???, ???cdh???, etc.) is made up of a diagonal in the matrix. If we add the first two columns of the matrix as new columns on the right side of the matrix,

then the first three terms, ???aei+bfg+cdh???, are given by

and the last three terms, ???-afh-bdi-ceg??? are given by

So this way of finding the determinant just requires us to expand the matrix by adding every column but the last column to the right side of the matrix, adding up the blue set of diagonal products, and then subtracting from that the yellow set of diagonal products.

The downside to this simple rule is that it only works this way for ???3\times3??? determinants. Let’s use the Rule of Sarrus on a ???3\times3??? matrix.

Example

Use the Rule of Sarrus to find the determinant.