How to find the area of any triangle
Area formula for different types of triangles
In this lesson we’ll look at how to find the area of a triangle, which is equivalent to half of the product of the base and the height.
???A=\frac{1}{2}bh???
The area is always in units of ???\text{length}^2??? (“length squared”).
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
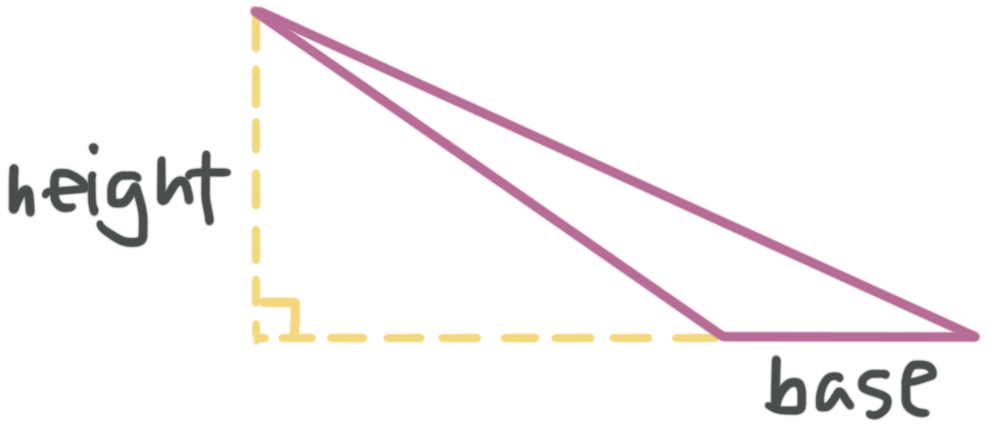
Any side of a triangle can be the base, but once you’ve chosen the base, the height is drawn from the opposite vertex (the vertex opposite the base) to the side that you’re using as the base. The height could look different depending on the type of triangle, but it’s always perpendicular to the base (in some cases perpendicular to an extension of the base).
In a scalene triangle, the lengths of all three sides are different.
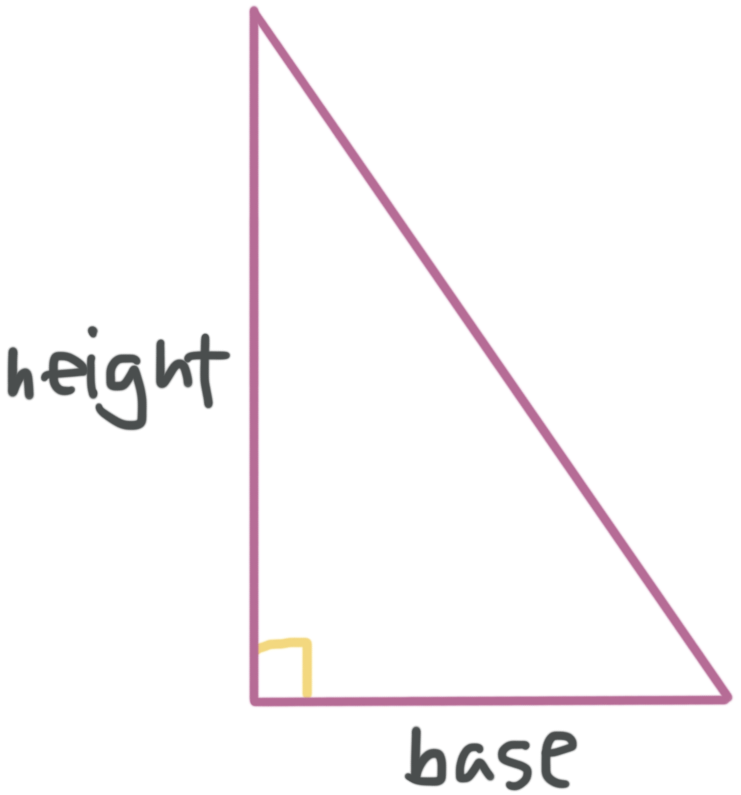
In a right triangle, one of the interior angles is a right (???90^\circ???) angle.
In an isosceles triangle, the lengths of exactly two sides are equal.
In an equilateral triangle, the lengths of all three sides are equal.
How to find the area of every kind of triangle
Take the course
Want to learn more about Geometry? I have a step-by-step course for that. :)
Finding the area of a scalene triangle using height outside the triangle
Example
Find the area of the triangle.
The area formula for a triangle is
???A=\frac{1}{2}bh???
In the diagram, the base of the triangle is ???14\text{ feet}??? and the height is ???12\text{ feet}???. Plugging these into the area formula, we get
???A=\frac{1}{2}(14)(12)???
???A=84\text{ feet}^2???
Let’s do one more.
Any side of a triangle can be the base, but once you’ve chosen the base, the height is drawn from the opposite vertex (the vertex opposite the base) to the side that you’re using as the base.
Example
Find the area of the right triangle to the nearest tenth.
The area of a triangle is given by
???A=\frac{1}{2}bh???
We can see that the base of the triangle is ???6.1'???, but we’ll need to use the Pythagorean Theorem to find the height. We’ll sketch in the height,
and then plug everything into the Pythagorean Theorem.
???{{6.1}^{2}}+{{h}^{2}}={{10.8}^{2}}???
???37.21+{{h}^{2}}=116.64???
???{{h}^{2}}=79.43???
???h=\pm \sqrt{79.43}???
???h\approx \pm 8.9???
Since we’re looking for height, we only need the positive answer, ???h\approx 8.9???. Now we can plug into the area formula.
???A\approx \frac{1}{2}(6.1)(8.9)???
???A\approx 27.1\text{ feet}^2???