Adjacent and nonadjacent angles
What are adjacent angles?
In this lesson we’ll look at how to identify adjacent angles in a diagram and how to form angle names.
Hi! I'm krista.
I create online courses to help you rock your math class. Read more.
Adjacent angles
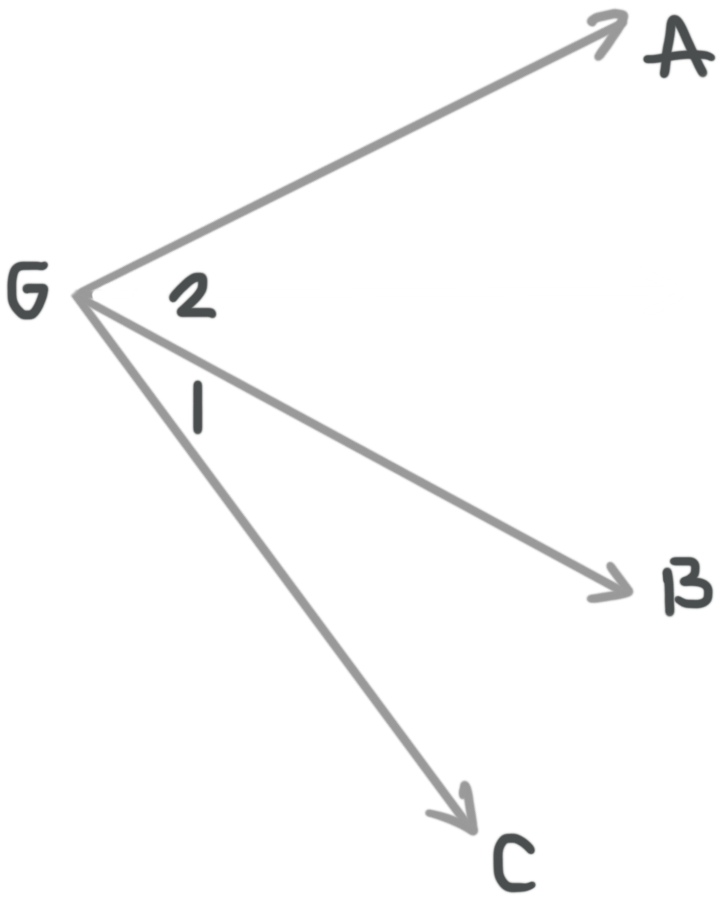
Adjacent angles share a common vertex and one common ray (or side).
In this diagram, angles ???1??? and ???2??? are adjacent because they share vertex ???G??? and ray ???\vec{GB}???.
Nonadjacent angles
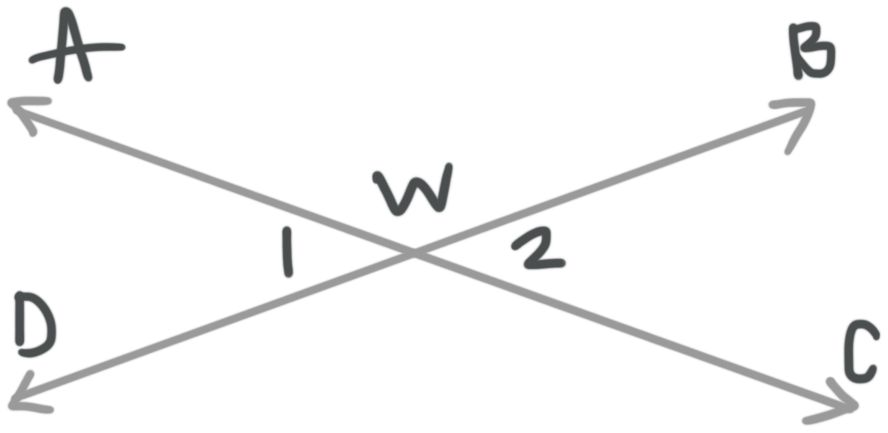
Nonadjacent angles may or may not share a common vertex, but they do not have any rays in common.
In this diagram, angles ???1??? and ???2??? are not adjacent, even though they share vertex ???W???, because they do not share a common ray.
Finding adjacent and nonadjacent angles
Take the course
Want to learn more about Geoemtry? I have a step-by-step course for that. :)
Finding pairs of adjacent angles with and without a diagram
Example
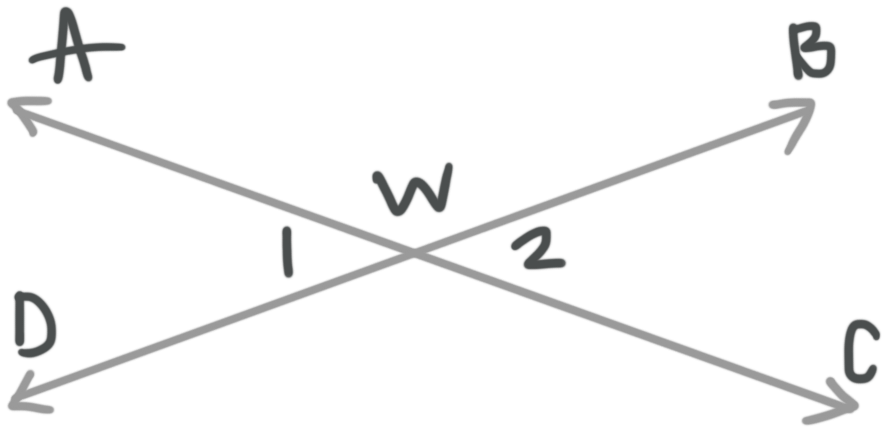
List the pairs of adjacent angles in the diagram.
Adjacent angles share a common vertex and a common ray.
???\angle DWA??? is adjacent to ???\angle AWB???; they share vertex ???W??? and ray ???\vec{WA}???.
???\angle DWA??? is adjacent to ???\angle DWC???: they share vertex ???W??? and ray ???\vec{WD}???.
???\angle DWC??? is adjacent to ???\angle CWB???; they share vertex ???W??? and ray ???\vec{WC}???.
???\angle CWB??? is adjacent to ???\angle AWB???; they share vertex ???W??? and ray ???\vec{WB}???.
Notice that you can tell from the way the angles are written which ray they share. For example,
???\angle CWB??? is adjacent to ???\angle AWB???; they share vertex ???W??? and ray ???\vec{WB}???. Since ???\angle AWB??? and ???\angle CWB??? both have the letters ???W??? and ???B??? from ray ???\vec{WB}???.
Let’s see about how to identify possible adjacent angles without a diagram.
Nonadjacent angles may or may not share a common vertex, but they do not have any rays in common.
Example
All of the angle pairs are from the same diagram. Classify each pair as adjacent or non-adjacent.
A. ???\angle ABC??? and ???\angle CBD???
B. ???\angle XYZ??? and ???\angle ZYX???
C. ???\angle LMN??? and ???\angle MNP???
D. ???\angle CED??? and ???\angle CEP???
Remember that adjacent angles have the same vertex and share one common ray. An angle name always has the vertex in the middle. You can then use the angle name to find the rays that make the angle.
Let’s look at each angle pair.
A. ???\angle ABC??? and ???\angle CBD???. Both of these angles share vertex ???B???. Now we need to look for one common ray. ???\angle ABC??? has rays ???\vec{BA}??? and ???\vec{BC}??? and ???\angle CBD??? has rays ???\vec{BC}??? and ???\vec{BD}???, which means that both angles share ray ???\vec{BC}???. Therefore, ???\angle ABC??? and ???\angle CBD??? are adjacent angles.
B. ???\angle XYZ??? and ???\angle ZYX???. Both of these angles share vertex ???Y???. Now we need to look for one common ray. ???\angle XYZ??? has rays ???\vec{YX}??? and ???\vec{YZ}??? and ???\angle ZYX??? has rays ???\vec{YZ}??? and ???\vec{YX}???, which means that both angles share rays ???\vec{YX}??? and ???\vec{YZ}???. Therefore, ???\angle XYZ??? and ???\angle ZYX??? are different ways to name the same angle.
C. ???\angle LMN??? and ???\angle MNP???. ???\angle LMN??? has vertex ???M??? and ???\angle MNP??? has vertex ???N???, so these angles do not share a vertex and they are nonadjacent.
D. ???\angle CED??? and ???\angle CEP???. Both of these angles share vertex ???E???. Now we need to look for one common ray. ???\angle CED??? has rays ???\vec{EC}??? and ???\vec{ED}??? and ???\angle CEP??? has rays ???\vec{EC}??? and ???\vec{EP}???, which means that both angles share ray ???\vec{EC}???. Therefore, ???\angle CED??? and ???\angle CEP??? are adjacent angles.